В данном месте земной поверхности все тела падают с одинаковым ускорением, обусловленным действием силы тяжести. Это ускорение называется ускорением свободного падения и обозначается  . Так как Земля не является идеальной сферой, то значение ускорения свободного падения зависит от географической широты места. Наибольшей величины оно достигает на полюсе (
. Так как Земля не является идеальной сферой, то значение ускорения свободного падения зависит от географической широты места. Наибольшей величины оно достигает на полюсе (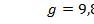 ), а наименьшего - на экваторе (
), а наименьшего - на экваторе (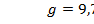 ). Средним значением считается величина, равная
). Средним значением считается величина, равная 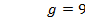 .
.
Непосредственное определение  из наблюдений свободного падения затрудняется тем, что время падения обычно мало. Поэтому для изучения
из наблюдений свободного падения затрудняется тем, что время падения обычно мало. Поэтому для изучения  часто пользуются наблюдением свободных гармонических колебаний математического маятника.
часто пользуются наблюдением свободных гармонических колебаний математического маятника.
Математическим маятником называют материальную точку, подвешенную на невесомой и нерастяжимой нити. Если на длинной тонкой нити подвесить металлический шарик, масса которого значительно больше, а размеры значительно меньше соответственно массы и размеров нити, то такой маятник можно считать математическим.
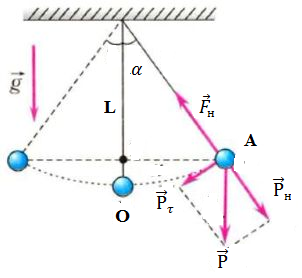
Рисунок 7.1-Силы, действующие на математический маятник в точке А
Выведем шарик из положения равновесия и отпустим. На шарик будут действовать две силы: сила тяжести  и сила натяжения нити
и сила натяжения нити  . Сила
. Сила  направлена вертикально вниз, а
направлена вертикально вниз, а  - вдоль нити. Силами сопротивления пренебрегаем. Разложим
- вдоль нити. Силами сопротивления пренебрегаем. Разложим  на две составляющие:
на две составляющие:  , направленную вдоль нити, и
, направленную вдоль нити, и  , направленную по касательной к траектории движения шарика (т.е. перпендикулярно нити). Равнодействующая сил
, направленную по касательной к траектории движения шарика (т.е. перпендикулярно нити). Равнодействующая сил  и
и  есть центростремительная сила, благодаря которой шарик движется по дуге окружности.
есть центростремительная сила, благодаря которой шарик движется по дуге окружности.
Под действием силы  маятник начинает двигаться вниз по дуге окружности к положению равновесия. По мере движения маятника, сила
маятник начинает двигаться вниз по дуге окружности к положению равновесия. По мере движения маятника, сила  , направленная к положению равновесия, уменьшается по модулю, и в тот момент, когда маятник проходит положение равновесия, она становится равной нулю. По инерции маятник проскакивает положение равновесия и поднимается вверх. Теперь составляющая
, направленная к положению равновесия, уменьшается по модулю, и в тот момент, когда маятник проходит положение равновесия, она становится равной нулю. По инерции маятник проскакивает положение равновесия и поднимается вверх. Теперь составляющая  меняет направление, но по прежнему направлена к положению равновесия. Тогда
меняет направление, но по прежнему направлена к положению равновесия. Тогда
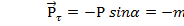 (7.1)
(7.1)
Знак «-» стоит потому, что  и
и  имеют противоположные знаки. При отклонении шарика вправо
имеют противоположные знаки. При отклонении шарика вправо  , а
, а  направлена влево и
направлена влево и  . При отклонении шарика влево
. При отклонении шарика влево  , а
, а  направлена вправо и
направлена вправо и  .
.
Обозначим через  касательное ускорение маятника. Тогда, согласно II закону Ньютона:
касательное ускорение маятника. Тогда, согласно II закону Ньютона:
 (7.2)
(7.2)
Подставляя (1.7) в (2.7), получаем:
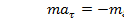 (7.3)
(7.3)
Из формулы (3) получаем:
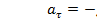 (7.4)
(7.4)
При малых 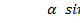 , следовательно,
, следовательно,
 (7.5)
(7.5)
Обозначим длину дуги  через
через  , тогда:
, тогда:
 , (7.6)
, (7.6)
откуда
 (7.7)
(7.7)
Подставляя (7.7) в (5.7) получим:
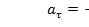 . (7.8)
. (7.8)
В уравнении (7.8)  - координата шарика,
- координата шарика,  - касательное ускорение; оно равно второй производной пути по времени. Тогда уравнение (7.8) можно записать в виде:
- касательное ускорение; оно равно второй производной пути по времени. Тогда уравнение (7.8) можно записать в виде:
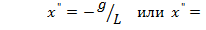 , (7.9)
, (7.9)
где
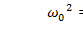 . (7.10)
. (7.10)
Из вида уравнения (7.9) следует, что координата (длина дуги)должна меняться со временем по закону синуса или косинуса, что можно проверить непосредственной подстановкой, и имеет вид
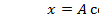 (7.11)
(7.11)
Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями. Следовательно, математический маятник совершает гармонические колебания, а составляющая силы тяжести  есть квазиупругая сила, вызывающая свободные гармонические колебания маятника.
есть квазиупругая сила, вызывающая свободные гармонические колебания маятника.
 - циклическая частота колебаний связана с периодом колебаний маятника
- циклическая частота колебаний связана с периодом колебаний маятника  :
:
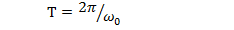 (7.12)
(7.12)
Из формулы (7.10)
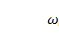 (7.13)
(7.13)
Отсюда:
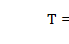 (7.14)
(7.14)
где  - ускорение свободного падения, а
- ускорение свободного падения, а  - длина нити математического маятника, т.е. расстояние от точки подвеса до центра тяжести шарика. Формула (7.14) может служить рабочей формулой для определения
- длина нити математического маятника, т.е. расстояние от точки подвеса до центра тяжести шарика. Формула (7.14) может служить рабочей формулой для определения  , но для нахождения
, но для нахождения  нужно знать радиус шарика.
нужно знать радиус шарика.
Чтобы исключить из опыта погрешность, связанную с измерением размеров шарика, поступают следующим образом: задают длину нити 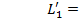 , затем, изменяя длину нити, измеряют
, затем, изменяя длину нити, измеряют 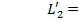 , где
, где  – радиус шарика. Тогда для периодов свободных колебаний
– радиус шарика. Тогда для периодов свободных колебаний  маятников двух разных длин
маятников двух разных длин  в соответствии с формулой(7.14) получаем:
в соответствии с формулой(7.14) получаем:
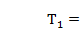 (7.15)
(7.15)
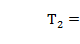 (7.16)
(7.16)
Или 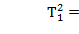 , (7.17)
, (7.17)
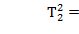 , (7.18)
, (7.18)
Далее:
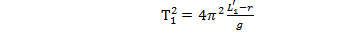
и 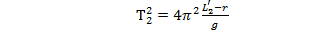
Вычитая из  выражение
выражение  , получаем путем простых преобразований выражение для ускорения:
, получаем путем простых преобразований выражение для ускорения:
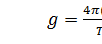 ,при
,при  . (7.19)
. (7.19)
Формула (7.19) есть рабочая формула для определения ускорения свободного падения.
 2018-03-09
2018-03-09 158
158








