2018-03-09
129
При кодировании сообщений считается, что символы сообщения порождаются некоторым источником информации. Источник считается заданным полностью, если дано вероятностное описание процесса появления сообщений на выходе источника. Это означает, что в любой момент времени определена вероятность порождения источником любой последовательности символов Р (x 1 x 2 x 3 ...xL), L ≥1. Такой источник называется дискретным вероятностным источником.
Если вероятностный источник с алфавитом А= { a 1, a 2,..., an }порождает символы алфавита независимо друг от друга, т.е. знание предшествующих символов не влияет на вероятность последующих, то такой источник называется бернуллиевским. Тогда для любой последовательности x 1 x 2 ... xL, L ≥1, порождаемой источником, выполняется равенство:
P (x 1 x 2 ... xL) = P (x 1)· P (x 2)·...· P (xL),
где P (x) – вероятность появления символа х, Р (x 1 x 2 x 3 ... xL) – вероятность появления последовательности x 1 x 2 x 3 ... xL.
Пусть имеется дискретный вероятностный источник без памяти, порождающий символы алфавита А ={ a 1,…, an } с вероятностями 
, 
. Основной характеристикой источникаявляется энтропия, которая представляет собой среднее значение количества информации в сообщении источника и определяется выражением (для двоичного случая):
.
Энтропия характеризует меру неопределенности выбора для данного источника.
Для практических применений важно, чтобы коды сообщений имели по возможности наименьшую длину. Основной характеристикой неравномерного кода является количество символов, затрачиваемых на кодирование одного сообщения. Пусть имеется разделимый побуквенный код для источника, порождающего символы алфавита А={ a 1, …, an } с вероятностями pi =P (ai), состоящий из n кодовых слов с длинами L 1, …, Ln в алфавите {0,1}. Средней длиной кодового слова называется величина 
, которая показывает среднее число кодовых букв на одну букву источника.
Побуквенный код называется разделимым (или однозначно декодируемым), если любое сообщение из символов алфавита источника, закодированное этим кодом, может быть однозначно декодировано.
Побуквенный разделимый код называется оптимальным, если средняя длина кодового слова минимальна среди всех побуквенных разделимых кодов для данного распределения вероятностей символов.
Побуквенный код называется префиксным, если в его множестве кодовых слов ни одно слово не является началом другого, т.е. элементарный код одной буквы не является префиксом элементарного кода другой буквы.
Избыточностью кода называется разность между средней длиной кодового слова и предельной энтропией источника сообщений
.
Избыточность кода является показателем качества кода, оптимальный код обладает минимальной избыточностью. Задача эффективного неискажающего сжатия заключается в построении кодов с наименьшей избыточностью, у которых средняя длина кодового слова близка к энтропии источника. К таким кодам относятся классические коды Хаффмана, Шеннона, Фано, Гилберта-Мура и арифметический код.
Основные теоремы побуквенного кодирования.
Теорема 1 (Крафт). Для того, чтобы существовал побуквенный двоичный префиксный код с длинами кодовых слов L 1, …, Ln, необходимо и достаточно, чтобы:
.
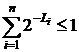Пример 1. Построить префиксный код с длинами L 1=1, L 2=2, L 3=2 для алфавита A= { a 1 ,a 2 ,a 3}. Проверим неравенство Крафта для набора длин
.
Неравенство выполняется и, следовательно, префиксный код с таким набором длин кодовых слов существует.
Теорема2 (МакМиллан). Для того чтобы существовал побуквенный двоичный разделимый код с длинами кодовых слов L 1,…, Ln, необходимо и достаточно, чтобы 
.
Метод оптимального побуквенного кодирования был разработан в 1952 г. Д. Хаффманом. Оптимальный код Хаффмана обладает минимальной средней длиной кодового слова среди всех побуквенных кодов для данного источника с алфавитом А= { a 1 ,…,an } и вероятностями pi =P (ai).
Рассмотрим алгоритм построения оптимального кода Хаффмана.
1. Упорядочим символы исходного алфавита А ={ a 1 ,…,an } по убыванию их вероятностей p 1 ≥ p 2 ≥ … ≥ pn.
2. Если А ={ a 1, a2}, то a 1 ® 0, a 2 ® 1.
3. Если А ={ a 1, …, aj, …, an } и известны коды < aj ® bj >, j = 1,…, n, то для алфавита { a 1 ,… 
, 
…,an } с новыми символами и вместо aj, и вероятностями p (aj) =p () + p (),код символа aj заменяется на коды ® bj 0, ® bj 1.
Пример 2. Пусть дан алфавит A={ a 1, a 2, a 3, a 4, a 5, a 6} с вероятностями
p 1=0.36, p 2=0.18, p 3=0.18, p 4=0.12, p 5=0.09, p 6=0.07.
Здесь символы источника уже упорядочены в соответствии с их вероятностями. Будем складывать две наименьшие вероятности и помещать суммарную вероятность на соответствующее место в упорядоченном списке вероятностей до тех пор, пока в списке не останется два символа. Тогда закодируем эти два символа 0 и 1. Далее кодовые слова достраиваются, как показано на рис. 1.
 |
a 1 0.36 0.36 0.36 0.36 0.64 0
a 2 0.18 0.18 0.28 0.36 0.36 1
a 3 0.18 0.18 0.18 0.28 00
a 4 0.12 0.16 0.18 000 01
a 5 0.09 0.12 010 001
a 6 0.07 0100 011
0101
Рис.1 – Процесс построения кода Хаффмана
Таблица 1
Код Хаффмана
| ai | pi | Li | кодовое слово |
| a 1 a 2 a 3 a 4 a 5 a 6 | 0.36 0.18 0.18 0.12 0.09 0.07 | 2 3 3 4 4 4 | 1 000 001 011 0100 0101 |
Средняя длина построенного кода Хаффмана:
Lср (P) = 1 . 0.36 + 3 . 0.18 + 3 . 0.18 + 3 . 0.12 + 4 . 0.09 + 4 . 0.07 = 2.44,
при этом энтропия данного источника равна:
H (p 1,…, p 6)= − 0.36 . log 0.36 − 2 . 0.18 . log 0.18 −0.12 . log 0.12 −
− 0.09 . log 0.09 − 0.07 . log 0.07 = 2.37.
Рис. 2 – Кодовое дерево для кода Хаффмана
Код Хаффмана обычно строится и хранится в виде двоичного дерева, в листьях которого находятся символы алфавита, а на «ветвях» – 0 или 1. Тогда уникальным кодом символа является путь от корня дерева к этому символу, по которому все 0 и 1 собираются в одну уникальную последовательность (рис. 2).
