Расширенный алгоритм Евклида

При заданных неотрицательных целых числах а и b этот алгоритм определяет вектор (u₁, u₂, u₃), такой, что a * u₁ + b * u₂ = u₃ = НОД (a, b).

В процессе вычисления используются вспомогательные векторы (v₁, v₂, v₃), (t₁, t₂, t₃). Действия с векторами производятся таким образом, что в течение всего процесса вычисления выполняются соотношения

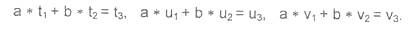
Для вычисления обратной величины a^-1(mod n) используется частный режим работы расширенного алгоритма Евклида, при котором

b = n, НОД(а,n) = 1, и этот алгоритм определяет вектор (u₁, u₂, u₃), такой, что

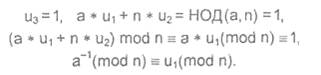
Шаги алгоритма:

1. Начальная установка.

Установить (u₁,u₂,u₃):= (0,1, n), (v_l, v₂, v₃):= (1, 0, a).

2. u₃ = 1?. Если u₃ = 1, то алгоритм заканчивается.

3. Разделить, вычесть.

Установить q:=[u₃/v₃].

Затем установить

(t₁, t₂, t₃):= (u₁,u₂,u₃) - (v₁, v₂, v₃) * q,

(u₁,u₂,u₃):= (v₁, v₂, v₃),

(v₁, v₂, v₃):= (t₁, t₂, t₃).
Возвратиться к шагу 2.

Пример

Заданы модуль n=23 и число а = 5. Найти обратное число

a^-1 (mod 23), т.е. x=5-1(mod23).

Используя расширенный алгоритм Евклида, выполним вычисления, записывая результаты отдельных шагов в таблицу 5.1.

 

Таблица 5.1 – Шаги расширенного алгоритма Евклида

q	u1	u2	u3	vl	v2	v3
4 1 1	0 1 -4 5 -9	1 0 1 -1 2	n = 23 5 3 2 1	1 -4 5 -9	0 1 -1 2	a = 5 3 2 1

 

При u₃ = 1, u₁ = -9, u₂= 2

(a * u₁ + n * u₂) mod n = (5 * (-9) + 23 * 2) mod 23 = 5* (-9) mod 23 ≡ 1,

a^-1 (mod n) = 5^-1 (mod 23) = (-9) mod 23 = (-9 + 23) mod 23 = 14.

Итак, x = 5^-1 (mod 23) = 14 (mod 23) = 14.

 

Алгоритм быстрого возведения в степень

Алгоритм быстрого возведения в степень — алгоритм, предназначенный для возведения числа x в натуральную степень n за меньшее число умножений, чем это требуется в определении.

Алгоритм не всегда оптимален. Например, при n=15 требуется 6 умножений, хотя на самом деле возведение в 15-ую степень можно выполнить за 5 умножений.

 

Теоретические основы алгоритма

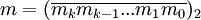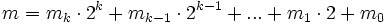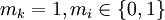Пусть — двоичное представление степени n. Тогда , где и .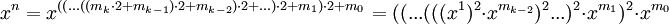

Таким образом, алгоритм быстрого возведения в степень сводится к мультипликативному аналогу схемы Горнера.

 

Оценка сложности

Чтобы узнать, сколько умножений потребуется для возведения числа x в степень n алгоритмом быстрого возведения в степень, нужно произвести вычисления по следующей формуле: k = H + 2(E − 1), где H — количество нулей, а E — количество единиц в двоичной записи числа n.

Так, для возведения числа в сотую степень этим алгоритмом потребуется всего лишь 8 умножений.

Таким образом количество умножений равно O(ln n).

Вычисление степени числа а по модулю n a^x mod n можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).

 

Пример

Нужно вычислить a⁸ mod n, не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:

(a * a * a * a * a * a * a * a) mod n

Вместо этого выполняют три малых умножения и три малых приведения по модулю:

((a² mod n)² mod n)² mod n.

Тем же способом вычисляют

a¹⁶ mod n = (((a² mod n)² mod n)²mod n)² mod n.

Вычисление a^x mod n, где х не является степенью 2, лишь немного сложнее. Двоичная запись числа х позволяет представить число х как сумму степеней 2: x = 25₍₁₀₎ = 1 1 0 0 1₍₂₎, поэтому 25 = 2⁴+ 2³ + 2⁰

Тогда a²⁵ mod n = (a * a²⁴) mod n = (a * a⁸ * a¹⁶) mod n =

= a * ((a²)²)² * (((a²)²)²)² mod n = ((((a² * a)²)²)² * a) mod n.

При разумном накоплении промежуточных результатов потребуется только шесть умножений:

(((((((a² mod n) * a) mod n)² mod n)² mod n)² mod n) * a) mod n

Этот метод уменьшает трудоемкость вычислений до 1,5xk операций в среднем, где k-длина числа в битах.

ВАРИАНТЫ ЗАДАНИЙ НА РГР

 

6.1 Задание №1

Сообщение S зашифровано по криптосистеме RSA с открытым ключом n и e, кроме того известна функция Эйлера 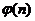. Дешифруйте сообщение. Исходные данные по вариантам заданы в таблице 6.1.

 

Таблица 6.1 - Шифрование по криптосистеме RSA. Варианты заданий.

№ вар.	S	n		e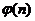
1	1721-301-619-1207	4187		977	4056
2	3890-2087-3110	5029		821	4876
3	0304-0903-3376-3508	4171		853	4032
4	2531-2930-732-2260	3589		713	3456
5	1981-276-1106	3599		703	3480
6	3890-2087-3110	5029		821	4876
7	5229-3908-1176-4103	5429		2099	5280
8	208-1497-793-96	2173		113	2080
9	3527-3312-542-1208	4189		911	4060
10	1499-3601-3292-2902	4453		937	4320
11	2294-4193-3345-852	4757		941	4620
12	1093-3587-2558-3981	5063		967	4920
13	782-1771-1476-4121	5029		887	4876
14	330-4126-3160-1828	5293		997	5148
15	1945-2991-286-1986	4717		827	4576
16	1149-444-3729-373	4187		821	4056
17	1721-301-619-1207	4187		977	4056
18	3890-2087-3110	5029		821	4876
19	0304-0903-3376-3508	4171		853	4032
20	2531-2930-732-2260	3589		713	3456
21	1981-276-1106	3599		703	3480
22	3890-2087-3110	5029		821	4876
23	5229-3908-1176-4103	5429		2099	5280
24	208-1497-793-96	2173		113	2080
25	3527-3312-542-1208	4189		911	4060
26	1499-3601-3292-2902	4453		937	4320
27	2294-4193-3345-852	4757		941	4620
28	1093-3587-2558-3981	5063		967	4920
29	782-1771-1476-4121	5029		887	4876
30	330-4126-3160-1828	5293		997	5148
№ вар.	S	n		e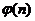
31	1945-2991-286-1986	4717		827	4576
32	1149-444-3729-373	4187		821	4056
33	1721-301-619-1207	4187	977		4056
34	3890-2087-3110	5029	821		4876
35	0304-0903-3376-3508	4171	853		4032
36	2531-2930-732-2260	3589	713		3456
37	1981-276-1106	3599	703		3480
38	3890-2087-3110	5029	821		4876
39	5229-3908-1176-4103	5429	2099		5280
40	208-1497-793-96	2173	113		2080
41	3527-3312-542-1208	4189	911		4060
42	1499-3601-3292-2902	4453	937		4320
43	2294-4193-3345-852	4757	941		4620
44	1093-3587-2558-3981	5063	967		4920
45	782-1771-1476-4121	5029	887		4876
46	330-4126-3160-1828	5293	997		5148
47	1945-2991-286-1986	4717	827		4576
48	1149-444-3729-373	4187	821		4056
49	1721-301-619-1207	4187	977		4056
50	3890-2087-3110	5029	821		4876
51	0304-0903-3376-3508	4171	853		4032
52	2531-2930-732-2260	3589	713		3456
53	1981-276-1106	3599	703		3480
54	3890-2087-3110	5029	821		4876
55	5229-3908-1176-4103	5429	2099		5280
56	208-1497-793-96	2173	113		2080
57	3527-3312-542-1208	4189	911		4060
58	1499-3601-3292-2902	4453	937		4320
59	2294-4193-3345-852	4757	941		4620
60	1093-3587-2558-3981	5063	967		4920
61	782-1771-1476-4121	5029	887		4876
62	330-4126-3160-1828	5293	997		5148
63	1945-2991-286-1986	4717	827		4576
64	1149-444-3729-373	4187	821		4056
65	1721-301-619-1207	4187	977		4056
66	3890-2087-3110	5029	821		4876
67	0304-0903-3376-3508	4171	853		4032
68	2531-2930-732-2260	3589	713		3456
№ вар.	S	n		e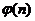
69	1981-276-1106	3599	703		3480
70	3890-2087-3110	5029	821		4876
71	5229-3908-1176-4103	5429	2099		5280
72	208-1497-793-96	2173	113		2080
73	3527-3312-542-1208	4189	911		4060
74	1499-3601-3292-2902	4453	937		4320
75	2294-4193-3345-852	4757	941		4620
76	1093-3587-2558-3981	5063	967		4920
77	782-1771-1476-4121	5029	887		4876
78	330-4126-3160-1828	5293	997		5148
79	1945-2991-286-1986	4717	827		4576
80	1149-444-3729-373	4187	821		4056
81	1721-301-619-1207	4187	977		4056
82	3890-2087-3110	5029	821		4876
83	0304-0903-3376-3508	4171	853		4032
84	2531-2930-732-2260	3589	713		3456
85	1981-276-1106	3599	703		3480
86	3890-2087-3110	5029	821		4876
87	5229-3908-1176-4103	5429	2099		5280
88	208-1497-793-96	2173	113		2080
89	3527-3312-542-1208	4189	911		4060
90	1499-3601-3292-2902	4453	937		4320
91	2294-4193-3345-852	4757	941		4620
92	1093-3587-2558-3981	5063	967		4920
93	782-1771-1476-4121	5029	887		4876
94	330-4126-3160-1828	5293	997		5148
95	1945-2991-286-1986	4717	827		4576
96	1149-444-3729-373	4187	821		4056
97	1721-301-619-1207	4187	977		4056
98	3890-2087-3110	5029	821		4876
99	0304-0903-3376-3508	4171	853		4032
100	2531-2930-732-2260	3589	713		3456
101	1981-276-1106	3599	703		3480
102	3890-2087-3110	5029	821		4876
103	5229-3908-1176-4103	5429	2099		5280
104	208-1497-793-96	2173	113		2080
105	3527-3312-542-1208	4189	911		4060
106	1499-3601-3292-2902	4453	937		4320
№ вар.	S	n		e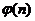
107	2294-4193-3345-852	4757	941		4620
108	1093-3587-2558-3981	5063	967		4920
109	782-1771-1476-4121	5029	887		4876
110	330-4126-3160-1828	5293	997		5148
111	1945-2991-286-1986	4717	827		4576
112	1149-444-3729-373	4187	821		4056
113	1721-301-619-1207	4187	977		4056
114	3890-2087-3110	5029	821		4876
115	0304-0903-3376-3508	4171	853		4032
116	2531-2930-732-2260	3589	713		3456
117	1981-276-1106	3599	703		3480
118	3890-2087-3110	5029	821		4876
119	5229-3908-1176-4103	5429	2099		5280
120	208-1497-793-96	2173	113		2080
121	3527-3312-542-1208	4189	911		4060
122	1499-3601-3292-2902	4453	937		4320
123	2294-4193-3345-852	4757	941		4620
124	1093-3587-2558-3981	5063	967		4920
125	782-1771-1476-4121	5029	887		4876
126	330-4126-3160-1828	5293	997		5148
127	1945-2991-286-1986	4717	827		4576
128	1149-444-3729-373	4187	821		4056

 

Примечание 1. В задании для преобразования слов, состоящих из букв русского алфавита (33 буквы) и пробелов, используются соответствия между символами и числами. Пробел заменяется на 1, буква А – на 2, буква Б – на 3 и т. д., буква Я заменяется на 34. Соответствующие числа, записанные в обратном порядке, образуют числовое представление открытого текста. Например, слову ДОМ будет соответствовать число 151706.

 

Таблица 6.2 – Алфавит

<пробел>	А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Н	О	П	Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30

 

Продолжение таблицы 6.2

Ь	Э	Ю	Я
31	32	33	34

 

Примечание 2. Для вычисления секретного ключа d рекомендуется использовать расширенный алгоритм Евклида, а для возведения чисел в степень по модулю n целесообразно использовать алгоритм быстрого возведения в степень.

 

Задание №2

Провести идентификацию для абонента А абонентом В используя систему иденти-фикации Гиллоу-Куинскуотера. Исходные данные по вариантам заданы в таблице 6.3

 

Таблица 6.3 -Система идентификации Гиллоу-Куинскуотера. Варианты заданий.