Требования, предъявляемые к информационному материалу

К собранному материалу предъявляются требования:

1. Информация должна обеспечивать однородность исследуемой совокупности, т.е. в одну совокупность нельзя включать объекты, характер и условия производства которых резко отличаются (например, сельскохозяйственная организация общественного сектора и фермерское хозяйство; ларек и супермаркет). В одну совокупность можно включать организации, имеющие приблизительно одинаковые природно-экономические условия, форму собственности, направление специализации.

2. Информация должна быть репрезентативной, т.е. иметь те же характеристики, что и генеральная совокупность. Это обеспечивается вышеизложенными во втором вопросе формулами.

3. Информация должна быть достоверной, т.е. не должна содержать ошибок. Экономическая информация в основном отвечает закону нормального распределения.

Для большинства экономических показателей характерно распределение данных, близкое к нормальному. Нормальным распределением называется такое, которое получается из ряда наблюдений, вариация которых обусловлена воздействием большого числа мелких беспорядочных или случайных влияний.

Используя формулы асимметрии (А) и эксцесса (Э), проверяют данные на соответствие их требованиям закона нормального распределения:

где – номер варианта опыта (объекта, элемента);

– множество вариантов опытов (объектов, элементов);

– фактическое значение факторного признака;

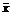– среднее значение факторного признака;

– число вариантов опыта;

– среднее квадратическое отклонение.

Среднее квадратическое отклонение определяют по одной из формул:

Информация не противоречит требованиям закона нормального распределения, если фактические значения А и Э равны нулю или не противоречат условию

где – квадратические отклонения или стандартные ошибки асимметрии и эксцесса.

* Формулы распространяются и на результативный показатель y.

Стандартные ошибки асимметрии и эксцесса определяются по следующим формулам:

Если асимметрия или эксцесс выходят за допустимые границы, проверяют, нет ли среди данных резко выделяющихся значений.

`х

`х-s_х

`х-3s_х

Кривая нормального распределения представлена на рис. 2.2. Как видно из рисунка, наиболее часто встречаются значения признака, близкие к его среднему. По мере удаления от среднего значения число наблюдений или вероятность наступления события уменьшаются. Причем в интервал от ` х-s_х до ` х+s_х попадает 68,26% случаев; от ` х- 2 s_х до ` х+ 2 s_х – 95,46%; от ` х- 3 s_х до ` х+ 3 s_х – 99,73% случаев. Поскольку в последний интервал попадает подавляющее большинство случаев при нормальном распределении, проявляется так называемое правило «трех сигм».

Считается, что данные принадлежат выборке, если .

В случае невыполнения условия для какого-то наблюдения или наблюдений их информацию исключают из выборки и вновь проверяют оставшиеся данные на соответствие требованиям закона нормального распределения.