I форма. В поперечных сечениях бруса при центральном растяжении (сжатии) нормальные напряжения равны отношению продольной силы к площади поперечного сечения:

II форма. Относительная продольная деформация прямо пропорциональна нормальному напряжению 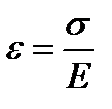 , откуда
, откуда 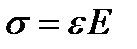 .
.
Как определяются напряжения в поперечных и наклонных сечениях бруса?
 – сила, равная произведению напряжения
– сила, равная произведению напряжения  на площадь наклонного сечения
на площадь наклонного сечения  :
:
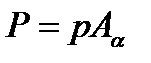


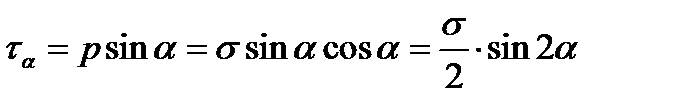
По какой формуле можно определить абсолютное удлинение (укорочение) бруса?
Абсолютное удлинение (укорочение) бруса (стержня) выражается формулой:
 , т.е.
, т.е. 
Учитывая, что величина  представляет собой жесткость поперечного сечения бруса длиной
представляет собой жесткость поперечного сечения бруса длиной  можно сделать вывод: абсолютная продольная деформация прямо пропорциональна продольной силе и обратно пропорциональна жесткости поперечного сечения. Этот закон впервые сформулировал Гук в 1660 году.
можно сделать вывод: абсолютная продольная деформация прямо пропорциональна продольной силе и обратно пропорциональна жесткости поперечного сечения. Этот закон впервые сформулировал Гук в 1660 году.
Как определяются температурные деформации и напряжения?
При повышении температуры у большинства материалов механические характеристики прочности уменьшаются, а при понижении температуры – увеличиваются. Например, у стали марки Ст3 при 
 и
и  ;
;
при 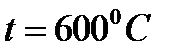
 и
и  , т.е.
, т.е.  .
.
Удлинение стержня при нагревании определяется по формуле  , где
, где  - коэффициент линейного расширения материала стержня,
- коэффициент линейного расширения материала стержня,  - длина стержня.
- длина стержня.
Возникающее в поперечном сечении нормальное напряжение  . При понижении температуры происходит укорочение стержня и возникают напряжения сжатия.
. При понижении температуры происходит укорочение стержня и возникают напряжения сжатия.
 2018-03-09
2018-03-09 490
490








