Невозмущенное движение. Задача двух тел

 

Наиболее популярной и наиболее изученной задачей небесной механики является задача двух тел: изучить движение материальной точки в гравитационном поле другой материальной точки, если известны массы этих точек, а также их положения и скорости в некоторый заданный момент времени. К задаче двух тел относятся, очевидно, задачи расчета движения небесного тела в гравитационном поле другого небесного тела, если несферичностью формы и несферичностью распределения плотности этих двух тел, а также воздействием гравитационных полей всех прочих небесных тел можно пренебречь.

Определение 3.1. Движение материальной точки в гравитационном поле другой материальной точки в условиях задачи двух тел называется невозмущенным или кеплеровым движением, а траектория этой материальной точки — орбитой кеплерова движения или, короче, кеплеровой орбитой.

Важным частным случаем задачи двух тел является задача изучения движения спутника в гравитационном поле некоторого притягивающего центра с известной массой. Эта задача называется ограниченной задачей двух тел.

Рассмотрим задачу двух тел подробнее. Пусть C и S — две материальные точки массами M и m соответственно, r_o(C) и r_o(S) — радиус-векторы этих точек в некоторой инерциальной системе координат Ox_o y_o z_o (рис. 3). Положение точки S относительно точки C будем определять вектором r = r_o(S) – r_o(C).

Согласно закону всемирного тяготения (2.3), на точку S со стороны точки C будет действовать сила гравитационного притяжения

 

 

 

 

где r = /r/; r/r - вектор единичной длины, определяющий направление гравитационной силы; μs = Gm — постоянная, называемая гравитационным параметром точки S. Соответственно на точку C со стороны точки S будет действовать такая же по величине и обратная по направлению сила

 

 

где μc = GM — гравитационный параметр точки C. Тогда уравнения движения точек S и C в системе координат Oxyz запишутся в виде

 

Рассмотрим некоторую декартову систему координат Cxyz, начало которой совпадает с притягивающим центром C. Тогда полученное равенство является выражением для ускорения точки S в системе координат Cxyz и приводит к важному выводу: движение материальной точки массой m относительно другой материальной точки массой M в задаче двух тел эквивалентно движению спутника в ограниченной задаче двух тел относительно притягивающего центра массой M + m. Величина гравитационного параметра спутника в ограниченной задаче двух тел будет равна μ = G(M + m). Так как масса спутника пренебрежимо мала по сравнению с массой притягивающего центра, то можно считать μ ≈ GM и

 

 

Это равенство называется уравнением движения спутника в ограниченной задаче двух тел.

Обозначим через    вектор скорости спутника и рассмотрим вектор , называемый вектором состояния. Рассмотрим также вектор

 

 

Тогда уравнение (3.1) в векторной форме будет записываться в виде

 

 

Интеграл энергии.

Умножим обе части уравнения (3.1) скалярно на величину

 

 

Это равенство можно записать в виде

 

Интегрируя левую и правую части последнего равенства по времени, получим выражение

 

 

где h — некоторая постоянная величина. Данное выражение называется интегралом энергии. Первое слагаемое в левой части представляет собой удвоенную кинетическую энергию единицы массы спутника, а второе слагаемое — удвоенную потенциальную энергию единицы массы спутника. Следовательно, постоянная h равна удвоенной величине полной энергии единицы массы спутника. Эта величина называется постоянной энергии.

Из формулы (3.2) следует, что полная энергия в задаче двух тел является постоянной величиной. В частности, это означает, что при удалении спутника от притягивающего центра его скорость уменьшается, а при приближении к притягивающему центру — увеличивается.

 

Интеграл площадей.

Предположим вначале, что векторы r и υ неколлинеарны, т. е. 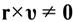. Умножим обе части уравнения движения спутника (3.1) векторно на величину r:

 

 

так как по определению векторного произведения

Продифференцируем теперь по времени выражение :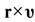

 

 

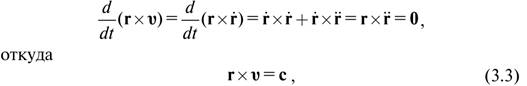
где c — некоторый постоянный вектор. Полученное равенство называется векторным интегралом площадей, а вектор c — векторной постоянной площадей. Как видно из последнего равенства, вектор r во время движения всегда остается ортогональным вектору c, т. е. вектор r всегда находится в плоскости, проходящей через притягивающий центр и определяемой нормальным к ней постоянным вектором c. Таким образом, интеграл площадей показывает, что движение спутника в ограниченной задаче двух тел происходит в одной плоскости, проходящей через притягивающий центр. Эта плоскость, т. е. плоскость движения спутника, называется неизменяемой плоскостью Лапласа. Равенство (3.3) является общим уравнением плоскости Лапласа в векторной форме.

Введем в пространстве декартову систему координат Cxyz с началом в притягивающем центре C, причем оси Cx и Cy расположим в плоскости движения спутника, ось Cz направим вдоль вектора c (рис. 4).

Пусть радиус-вектор r и вектор скорости υ спутника в этой системе имеют координаты

 

                                                      (3.4)

 

Введем в плоскости движения полярные координаты , полагая

 

 

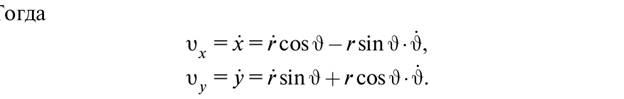
Подставляя эти равенства в выражение для третьей координаты в равенстве (3.4), получим после преобразований соотношение

 

 

которое называется полярной формой интеграла площадей. Эта формула имеет несколько важных следствий:

1. Если направление оси Cz совпадает с направлением вектора c, т. е. c > 0, то в любой момент времени t справедливо условие 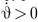. Это означает, что угол наклона радиус-вектора спутника по отношению к оси Cx постоянно возрастает и движение спутника происходит в положительном направлении (т. е. в направлении против часовой стрелки, если смотреть на плоскость Cxy со стороны положительного направления оси Cz). Такое движение спутника называется прямым. Если же c < 0, то движение спутника все время происходит в отрицательном направлении, и такое движение называется обратным.

2. Из полярной формы интеграла площадей (3.5) следует выражение для угловой скорости спутника

 

которое показывает, что, чем дальше спутник от притягивающего центра, тем меньше его угловая скорость.

3. Пусть радиус-вектор спутника за время Δt успел описать некоторый угол ∆J и «замести» некоторую площадь ΔS. Площадь заметенного сектора ΔS приближенно равна

 

т. е. секториальная скорость невозмущенного движения спутника относительно притягивающего центра постоянна.

Полученный результат выражает второй закон Кеплера: за равные промежутки времени радиус-вектор спутника заметает сектора равной площади.

 

Замечание 3.1. При выводе формулы интеграла площадей предполагалось, что векторы r и υ неколлинеарны. Легко показать, что в случае коллинеарности этих векторов спутник будет совершать прямолинейное движение в направлении своего радиус-вектора, и понятие плоскости движения теряет смысл..

 

 

Интеграл Лапласа.