Квантование магнитного потока

       

Рассмотрим волновую функцию куперовских пар:

   ,

где  – амплитуда волновой функции,

 – концентрация куперовских пар,

 – фаза волновой функции.

 

При наличии магнитного поля обобщенный импульс куперовских пар можно записать как:

.

Так как , то .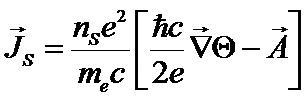

Введем обозначение  – квант магнитного потока,

тогда получим

 – квантовое обобщение 2-го уравнения Лондонов.

 

 

Рассмотрим массивное сверхпроводящее кольцо.

Если сверхпроводник охладить в магнитном поле, то в кольце заморозится некоторый магнитный поток Ф, который будет создаваться экранирующим сверхтоком, текущим по внутренней стороне кольца.

 

 

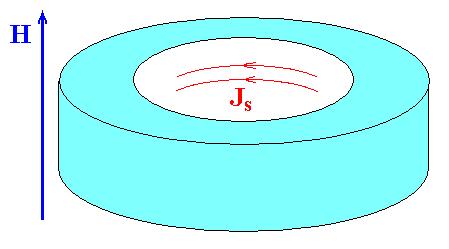
Рассмотрим замкнутый контур L, охватывающий сверхток.

 

Тогда интегрирование 2-го уравнения Лондонов по контуру L дает:

 

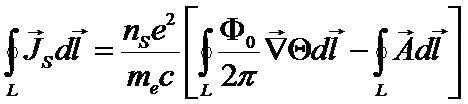
Так как контур L находится за областью сверхтока, то

=>  

=> .

 

По определению .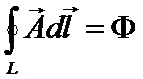

=> .

 

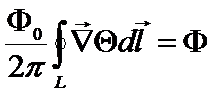!!! Так как  – фаза волновой функции, то при каждом обходе контура  меняется на 2π

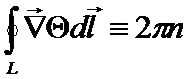=> , где

Тогда      =>

 

Магнитный поток через сверхпроводящее кольцо (или любую полость в сверхпроводнике) может принимать только значения, кратные кванту магнитного потока.

Физически это означает, что по кольцу должно укладываться целое число длин волн волновой функции куперовских пар.