Глубина проникновения магнитного поля

Электродинамика СП

Уравнения Лондонов.

1) Рассмотрим сверхпроводник во внешнем электрическом и магнитном поле. Поля должны быть малы, чтобы они не повлияли на концентрацию носителей сверхтока n_S.

 

Закон Ньютона (для куперовских пар):

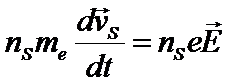
Так как плотность сверхтока

=>

 

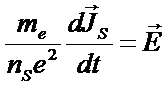
Введем обозначение:

=>  – 1-е уравнение Лондонов

 

1-е уравнение Лондонов связывает сверхток с электрическим полем.

Следствие из 1-го уравнения Лондонов:

В стационарном состоянии (т.е. при ) напряженность электрического поля в сверхпроводнике равна нулю.

 

2) Выведем 2-е уравнение Лондонов, связывающее сверхток с магнитным полем.

! даже в слабых магнитных полях (Н << Н_С) в тонкий слой сверхпроводника внешнее магнитное поле проникает, индуцируя экранирующий сверхток.

 

Без магнитного поля и сверхтока плотность свободной энергия сверхпроводника равна ,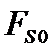

а при наличии магнитного поля и сверхтока

где  – плотность энергии магнитного поля,

а  – плотность энергии сверхтока (кинетическая энергия куперовских пар).

 

 

Найдем выражение для плотности энергии сверхтока.

 

С учетом 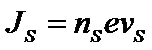, получим

 

Учтем, что сверхток индуцирован магнитным полем и воспользуемся уравнением Максвелла:

.

Тогда  

Введем обозначение:   .

Тогда

Теперь можем записать выражение для полной свободной энергии сверхпроводника:

Теперь решим уравнение .

В итоге, опуская чудовищные вычисления, получаем:

    – 2-е уравнение Лондонов.

 

Можно 2-е уравнение представить в более компактной форме.

С учетом    и , получим:

   – тоже 2-е уравнение Лондонов.

! Но, при такой записи нужно учитывать «лондоновскую» калибровку векторного потенциала А:

и , где n – нормаль поверхности СП.

 

С учетом       и

 

получим еще одну форму 2-го уравнения Лондонов:

Связь между лондоновскими параметрами

 

Глубина проникновения магнитного поля.

       

Рассмотрим сверхпроводник в магнитном поле

 

Воспользуемся вторым уравнением Лондонов в форме

.

Для одномерного случая (вдоль оси Х):

.

   Решением этого уравнения является:

   .

       

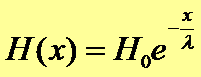Как видим, магнитное поле спадает экспоненциально, а смысл параметра λ в том, что на расстоянии λ от границы сверхпроводника магнитное поле ослабляется в е раз.

 

Параметр λ называют лондоновской глубиной проникновения и часто пишут как λ_L.

 

В формуле для λ входит концентрация куперовских пар, которая является функцией температуры    => λ = f(T).

   Для чистых металлических сверхпроводников хорошо работает эмпирическая формула:

  

   Для многих металлических сверхпроводников

   .