Дифракционных решетках

ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ СВЕТА И УЛЬТРАЗВУКА

ДИФРАКЦИОНЫМ МЕТОДОМ

 

Цель работы – определение длин световых волн в спектре излучения паров ртути с помощью дифракционной решетки, а также измерение длины волны ультразвука и скорости его распространения в жидкости по наблюдению дифракции света на ультразвуковой волне.

 

Дифракция света на амплитудной и фазовой

дифракционных решетках

Вначале рассмотрим дифракцию света на амплитудной дифракционной решетке, которая представляет собой систему эквидистантно расположенных в одной плоскости параллельных прямых щелей с непрозрачными промежутками между ними. Прозрачность такой решетки периодически изменя­ется вдоль направления, перпендикулярного к щелям (штрихам) решетки, в результате чего амплитуда световой волны сразу за решеткой также изменяется периодически.

Распределение дифракционного поля рассчитывают на основе принципа Гюйгенса – Френеля и принципа линейной суперпозиции полей: каждая точка волнового фронта является источником вторичных сферических волн, результирующее поле в каждой точке есть сумма векторов напряженности составляющих сферических волн. Исходя из этого процесс образования дифракционной картины условно можно раз­бить на два этапа. На первом этапе свет, проходя через дифрак­ционную решетку, испытывает дифракцию на каждой из N ще­лей. На экране Э образуется N одинаковых дифракционных картин. Эти картины накладываются одна на другую. Вторым этапом можно считать интерференцию в плоскости экрана N соответствующих волн, в результате которой возникают дополнительные максиму­мы и минимумы, отсутствующие в дифракционной картине от одной щели. Действительно, рассмотрим для примера интерференцию полей, созданных парами точек двух щелей (рис. 1). Результирующая напряженность электрического поля световой волны в точке наблюдения Р экрана Э равна

 ,                   (1)

где – изменение фазы соответствующей сферической волны при пробеге от плоскости щелей до точки наблюдения. Можно сначала сгруппировать слагаемые по каждой щели:

          (2)

Видно, что результирующее поле, созданное в точке Р каждой щелью,  или , зависит от разности фаз полей только этой щели  или  соответственно. При перемещении точки наблюдения Р по экрану разности фаз меняются, меняются и величины , , т.е. наблюдается распределение поля при дифракции на щели. Дальнейшее суммирование полей в (2)

                           (3)

показывает, что результирующее поле в точке наблюдения зависит от разности фаз  полей двух щелей. Более подробное суммирование полей приведено в работах [1, 2].

Будем рассматривать частный слу-чай дифракции, называе­мый дифракцией Фраунгофера. Дифракция Фраунгофера наблю­дается тогда, когда на препятствие, вызывающее дифракцию, па­дает пучок параллельных лучей и наблюдение ведется в точке, где сходятся практически параллельные лучи. Это осуществляет­ся, например, когда источник света и точка наблюдения бесконечно удалены от указанного препятствия. Для наблюдения дифракции Фраунгофера на лабораторной установке конечных размеров необходимо источник света поместить в передней фокальной плоскости собирающей линзы, а наблюдение вести в задней фокальной плоско­сти другой собирающей линзы, расположенной за дифракционным препятствием (см. подробнее в описании экспериментальной установки).

Рассмотрим сначала дифракцию Фраунгофера на одной щели Щ (рис. 2). Соответствующее дифракционное распределение интенсивности, возникающее на экране Э, расположенном в задней фокальной плоскости линзы Л, подробно описано в лабораторной работе № 30.

Если щель сместить вправо или влево, то дифракционная картина не изменится, так как в соответствии с законами гео­метрической оптики останутся на прежних мес­тах как фокус точки , т.е. точка фокусировки пучка, параллельного оси линзы, так и точка фокусировки  пучка, наклоненного к оси линзы под некоторым углом 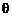 [3]. Из этого следует, что когда параллельный пучок света проходит сквозь дифракцион­ную решетку, состоящую из N одинаковых параллельных щелей,
N одинаковых дифракционных картин накладыва­ются в точности од-

на на другую. Волны, приходящие на экран от всех щелей, можно считать когерентными, так как в соответствии с принци­пом Гюйгенса­–Френеля они созданы вторичными источ­никами, принадлежащими единому фронту волны, испускаемой первичным источником. При сложении та­ких волн наблюдается интерференция. Для определения тех на­правлений дифрагированного света, для которых наблюдаются максимумы интенсивности, рассмотрим схему, представленную на рис. 3. На этом рисунке: ДР – дифракционная решетка; Л – линза; Э – экран; отрезок АВ – ширина щели; отрезок ВС – ширина пере­мычки между щелями. Величина  = АВ + ВС называется перио­дом или постоянной решетки. На рисунке показаны два луча, отклоненные за счет дифракции на одинаковый угол 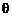, причем точки А и С, из которых вы-

 

ходят лучи, расположены в соседних щелях сходным образом (обе –
в крайней левой части щели). Сдвиг фаз между этими лучами определяется оптической разно­стью хода этих лучей. В нашем случае оптическая разность хода . Максимальная интенсивность результирующей волны наблюдается тогда, когда оптическая разность хода равна целому числу длин волн, т. е. при условии

                    , = 0, ±1, ±2 …                    (5)

Формула (5) была получена при рассмотрении только двух лу­чей, проходящих сходным образом через соседние щели. Однако этот результат справедлив и для лучей, проходящих сходным образом через все N щелей решетки. Аналогично можно рас­смотреть систему N лучей, проходящих сходным образом в лю­бой части щели, и убедиться, что формула (5) справедлива в об­щем случае. Максимумы, соответствующие направлениям, опре­деляемым формулой (5), называются главными максимумами или дифракционными порядками. Амплитуда колебаний в этих направлениях при дифракции на решетке в N раз больше, чем при дифракции на одной щели, а интенсивность света –
в N ² раз.

Для  угол 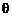 в (5) зависит от . Если излучение немонохроматично, в каждом ненулевом дифракционном порядке будут последовательно расположены максимумы для каждой спектральной линии. В этом и заключается спектральное разложение, осуществляемое дифракционной решеткой. При  уравнению (5) удовлетворяет только  и любое значение . Поэтому в нулевом порядке дифракции, в точке , максимумы всех спектральных линий совмещены: нулевой порядок бездисперсионный, «белый». Излучение разных спектральных линий взаимно некогерентно, поэтому на экране дифракционные картины для разных линий просто накладываются без какой-либо дополнительной интерференции.

Очевидно, что в направлениях, удовлетворяющих выраже­нию (4), для которых интенсивность света от одной щели равна нулю, интенсивность от всей решетки также равна нулю. Эти ми­нимумы называются главными минимумами. Более строгий расчет показывает, что между соседними главными максимумами находятся еще (N – 1) дополнительных минимумов, между ко­торыми располагаются дополнительные максимумы, однако интенсивность света в них мала по сравнению с интенсивностью в главных максимумах и на практике они наблюдаются редко.

 

Рассмотрим теперь фазовую дифракционную решетку. Один из вариантов фазовой дифракционной решетки показан на рис. 4. Решетка представляет собой прозрачную плоскопараллельную пластинку толщиной 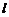. Показатель преломления этой пластинки периодически изменяется вдоль направления оси  с перио­дом . Ширина каждого элемента с постоянным значением показателя преломления равна .

 

Рис. 4

 

Амплитуда колебаний на выходной плоскости пластины остается одинаковой во всех ее точках. График зависимости фазы  волны на выходной плоскости от координаты  показан на рис. 5. Разность фаз лучей света, прошедших участки с разными показателями преломления, на выходе из пластинки определяется выражением

,                                            (6)

где  – разность показателей преломления соседних элементов решетки.

 

 

Рис. 5

 

Такую фазовую дифракционную решетку можно рассматривать как совокупность двух амплитудных реше­ток с одинаковыми периодами , но с разной фазой волны на выходе решетки. Так как периоды решеток одинаковы, угло­вые распределения дифрагированного света для этих решеток также одинаковы. Главные максимумы при дифракции на каждой из решеток должны наблюдаться при выполнении условия (5). Амплитуды главных максимумов зависят от разности фаз волн, созданных решетками. Предположим, фазовая решетка представляет собой однородный слой с постоянным показателем преломления, т.е. , . Тогда падающий на решетку плоский волновой фронт останется плоским как на выходе решетки, так и при последующем распространении. Эквивалентный плоской волне пучок лучей, параллельных оси, сфокусируется линзой в точку , следовательно, амплитуды высших дифракционных порядков ( = ±1, ±2 …) будут равны нулю. То же самое произойдет и при . Очевидно, максимум амплитуд высших порядков соответствует промежуточному значению

.

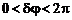Расчеты показывают, что максимум наблюдается при . Таким образом, с ростом разности фаз на решетке амплитуды высших дифракционных порядков меняются периодически.