Методические указания к выполнению лабораторных работ
по курсу: "Основы дискретной математики"
для студентов специальностей 091401, 092401
«Системы управления и автоматика»,
«Телекоммуникационные системы и сети»
Рассмотрен на заседании кафедры автоматики и телекоммуникаций.
Протокол № 11
от «22» октября 2010 р.
Утвержден на заседании научно-издательского совета ДонНТУ
Протокол № ___
от «___»___________2010 р.
Донецк, ДонНТУ 2010
УДК 681.3.07
Методические указания к лабораторным работам по курсу "Основы дискретной математики" для студентов специальностей 091401, 092401 «Системы управления и автоматика», «Телекоммуникационные системы и сети» / доц. Жукова Н.В., ас. Зайцева Э.Е. – Донецк, ДонНТУ. 2010. – 45 с.
Методические указания содержат лабораторные работы по основным разделам курса ОДМ и предназначены для студентов специальностей 091401, 092401 «Системы управления и автоматика», «Телекоммуникационные системы и сети».
Составитель доц. Жукова Н.В., ас. Зайцева Э.Е.
Рецензент доц. Ф-ту КНТ каф. АСУ Светличная В.А.
доц. Ф-ту КИТА каф. ЭТ Тарасюк В.П.
Ответственный за выпуск доц. Бессараб В.И.
Содержание
Лабораторная работа №1.
Множества, операции над множествами…………………...............……………4
Лабораторная работа №2.
Алгебра высказываний……………………………….................….…...................9
Лабораторная работа №3.
Минимизация булевых функций. Логические схемы……..……………………17
Лабораторная работа №4.
Конечные автоматы с памятью..…………………………………………………32
СПИСОК ЛИТЕРАТУРЫ…………………………………………………………45
Лабораторная работа № 1
Тема: «Множества, основные операции над множествами»
Цель: Приобретение практических навыков работы с множествами
1.1. Теоретические сведения [1].
Операции над множествами
Опишем основные способы получения новых множеств из уже имеющихся. Эти способы называются операциями над множествами.
Объединение множеств
Объединением множеств  и
и  называется множество, которое обозначается
называется множество, которое обозначается  (иногда
(иногда  ) и состоящее из всех тех и только тех элементов, которые принадлежат множеству
) и состоящее из всех тех и только тех элементов, которые принадлежат множеству  или множеству
или множеству 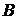 .
.
Приведем графическую иллюстрацию операции объединения двух множеств:


Выражение  читается: «объединение множества
читается: «объединение множества  и множества
и множества 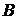 ». Часто операцию объединения двух множеств записывают в виде:
». Часто операцию объединения двух множеств записывают в виде:
 ,
,
который возможно использовать, учитывая, что множество элементов  – это множество «всех тех и только тех элементов, которые принадлежат множеству
– это множество «всех тех и только тех элементов, которые принадлежат множеству  или множеству
или множеству 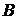 ».
».
Пересечение множеств
Пересечением множеств  и
и 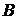 называется множество, которое обозначается
называется множество, которое обозначается  (иногда
(иногда  ) и состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств
) и состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств  и
и 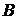 .
.
Приведем графическую иллюстрацию операции пересечения двух множеств:


Выражение  читается: «пересечение множества
читается: «пересечение множества  и множества
и множества 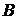 ».
».
Часто операцию пересечения двух множеств записывают в виде:
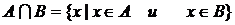 ,
,
который возможно использовать, учитывая, что множество элементов  – это множество «всех тех и только тех элементов, которые принадлежат каждому из множеств
– это множество «всех тех и только тех элементов, которые принадлежат каждому из множеств  и
и 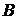 ».
».
Разность множеств
Рассмотрим операцию над множествами, которая определяется только для двух множеств.
Разностью множеств  и
и 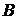 называется множество, которое обозначается
называется множество, которое обозначается  (иногда
(иногда 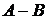 ) и состоящее из всех тех и только тех элементов множества
) и состоящее из всех тех и только тех элементов множества  , которые не является элементами множества
, которые не является элементами множества 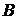 .
.
Приведем графическую иллюстрацию операции разности двух множеств:



Выражение  читается: «разность множества
читается: «разность множества  и множества
и множества 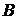 ».
».
Часто операцию разности двух множеств  и
и  записывают в виде:
записывают в виде:
 ,
,
который возможно использовать, учитывая, что множество элементов  – это множество «всех тех и только тех элементов множества
– это множество «всех тех и только тех элементов множества  , которые не являются элементами множества
, которые не являются элементами множества 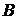 ».
».
Универсальное множество и дополнение множества
Как правило, при определении конкретного множества явно или неявно (интуитивно) ограничивается собрание допустимых объектов. Например, говоря о слонах, говорят о млекопитающих; говоря о натуральных числах, предполагают задание множества целых или действительных чисел.
Удобно совокупность допустимых объектов зафиксировать и считать, что рассматриваемые множества состоят из элементов этой совокупности. Искомую совокупность называют универсальным множеством или универсумом и обозначают  .
.
В соответствии с этим любое множество будем рассматривать в связи с универсумом, который при графической иллюстрации будем изображать прямоугольником, а множества будем изображать внутри данного прямоугольника.

В соответствии с введением множества  разность
разность  будем называть дополнением множества
будем называть дополнением множества  (до множества
(до множества  ) и обозначать
) и обозначать 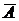 .
.
 2018-02-13
2018-02-13 251
251







