Моделирование задач оптики

В настоящее время широкое распространение получили приборы, принцип работы которых основан на преобразовании излучения различными типами оптических элементов. К этим приборам относятся фокусаторы, дифракционные решетки, волноводные элементы, элементы градиентной оптики, светоделители, резонаторы и т.д. При конструировании подобных элементов необходимо получать определенный набор параметров, без которых невозможно конструирование и разработка технологических процессов. В общем случае, распространение излучения описывается уравнением Максвелла (1.75 – 1.77).Уравнения Максвелла связывают вектор напряженности электрического поля E и вектор электрической индукции D с вектором напряженности магнитного поля H и вектором индукции B. В отсутствие токов и свободных электрических зарядов.

Подставим величину (1.76) в уравнение (1.77) и, предполагая, что величина не зависит от пространственных координат, возьмем ротор от левой и правой частей этого уравнения

. (1.2.7)

Используя уравнения (1.2.1) и (1.2.5), а также принимая во внимание, что

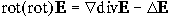, , (1.2.8)

можно переписать уравнение (1.2.7) в виде

. (1.2.9)

Присутствующий в соотношениях (1.2.8), (1.2.9) оператор является вектором с компонентами 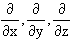. Если величина постоянна в пространстве, градиент обращается в нуль, и уравнение (1.2.9) принимает вид волнового уравнения

. (1.2.10)

Применяя операцию к обеим частям уравнения (1.2.1), можно получить аналогичное уравнение для

. (1.2.11)

Из (1.2.11) следует, что каждая декартова компонента Y w (x,y,z,t) вектора или B удовлетворяют скалярному волновому уравнению

, (1.2.12)

где величина v имеет физический смысл скорости света в среде с параметрами e и m

. (1.2.13)

Частным решением уравнения (1.2.12) может служить плоская волна произвольной формы, распространяющаяся в направлении n. Если в каждой точке пространства величина меняется во времени по гармоническому закону, то плоская волна может быть описана выражением

, (1.2.14)

где w - циклическая частота, а - амплитуда.

Вводя волновой вектор , модуль которого равен k =2p /l, выражению (1.2.14) можно придать вид

. (1.2.15)

В расчетах удобно пользоваться комплексным представлением плоской гармонической волны

. (1.2.16)

 

В комплексной форме могут быть представлены также расходящиеся и сходящиеся сферические волны, которые имеют соответственно вид

, (1.2.17)

. (1.2.18)

Поскольку нас интересует преимущественно монохроматическое излучение, то есть излучение определенной частоты, мы будем в дальнейшем опускать экспоненциальный множитель

.                                   (1.2.19)

Если зависимость от времени представляется в форме (1.2.19), то дифференцирование по времени заменяется умножением на -iw и волновое уравнение (1.2.12) принимает вид

,                                       (1.2.20)

где под Y следует понимать комплексную амплитуду волны. Уравнение (1.2.20) называется приведенным волновым уравнением Гельмгольца. В нашем курсе это уравнение играет фундаментальную роль. В последующих разделах нам придется неоднократно к нему обращаться в процессе анализа особенностей распространения волновых пучков в различных средах и оптических системах.

До сих пор обсуждение касалось волнового уравнения (1.2.12), полученного как частный случай уравнения (1.2.9). Поскольку первое из них является существенно более простым и удобным, возникает вопрос о возможности его применения также для случая неоднородных сред. Для ответа на этот вопрос следует определить, в каких случаях можно пренебречь вторым членом в уравнении (1.2.9). Доминирующими членами в уравнении (1.2.9) являются первый член в левой части и член в правой части, порядок величин которых одинаковый. Возьмем отношение второго члена левой части уравнения (1.2.9) к члену, стоящему в правой части

. (1.2.21)

Несложный анализ, выполненный в [8], показывает, что порядок R определяется соотношением

, (1.2.22)

где , - значения относительной диэлектрической проницаемости в двух близких точках, разделенных расстоянием , e - ее среднее значение. Выбирая =l, получаем

. (1.2.23)

Для того чтобы пренебречь вторым членом в левой части уравнения (1.2.9), необходимо потребовать выполнения условия R <<1. Это означает, что относительное изменение e на расстоянии длины волны должно быть много меньше 1. Для большинства неоднородных оптических сред такое условие хорошо выполняется, что позволяет ограничиваться решением уравнения (1.2.10) вместо (1.2.9). Только на границе раздела двух областей с различными диэлектрическими проницаемостями, например, на границе между стеклянными линзами и воздухом, величина R становится большой. Однако даже в этих случаях следует решать уравнение (1.2.10) или (1.2.12), так как оно справедливо всюду, кроме границы раздела сред. На практике обычно решают волновое уравнение в различных однородных областях и сшивают эти решения посредством граничных условий.

 К сожалению, данные уравнения, даже в самом простом виде очень трудно решить численно. Это связано с проблемами точности численных методов.

Как известно, для того, чтобы осуществлялась сходимость сеточного численного метода (например, метода Ньютона) размер сетки должен быть равен 1/4 характерного параметра (1/4 длины волны излучения). Это приводит к резкому увеличению объема памяти используемой компьютером для решения этих задач.

В тоже время, как показывает практика, различные аналитические решения с большой точностью описывают распространение излучения в среде при наличии правильного формирования функции передачи исследуемого объекта. При этом, все практические задачи можно разделить на два класса:

1. Прямые задачи оптики.

2. Обратные задачи оптики.

Прямые задачи оптики формулируются следующим образом – известно поле до объекта, известно как это поле преобразуется объектом, необходимо определить, как это поле записывается приемником излучения. Математически, это записывается следующим образом:

,                       (3.1)

где Е₀ – параметр поля (напряженность, фаза, интенсивность и т.д.) до объекта;

А – оператор перехода, описывающий изменение поля на объекте, который часто называют передаточной функцией объекта;

Е₁ – поле в устройстве регистрации (фотоприемник, экран).

В нашей задаче Е₀ и А известны, требуется определить Е₁.

Прямые задачи оптики достаточно хорошо решаются, однако, при разработке элементов чаще требуется решение обратных задач оптики, которые можно сформулировать следующим образом – задано поле до объекта, задано поле в приемнике излучения, необходимо подобрать объект, который изменяет это поле заданным образом. В математической постановке – это требование найти оператор А или передаточную функцию объекта.

Данные задачи решаются достаточно сложно и относятся к классу некорректно поставленных задач. Чаще всего для решения подобных проблем применяют следующий прием – разбивают интересующий нас объект на несколько объектов, функция передачи (волновая функция) которых известна или рассчитывается несложным образом. Общая функция передачи этих объектов определяется с помощью законов геометрической оптики и представляет собой матрицу, порядок которой определяется размерностью системы. Таким образом, мы сводим обратные задачи оптики к прямым задачам. В данном курсе будет рассмотрено только одно приближение решений уравнения Максвелла, для так называемого, когерентного излучения, поскольку именно в таком приближении описывается чаще всего  распространение лазерного излучения при моделировании простейших элементов оптики. Однако принципиально данная методика применима к приближению любого типа.