Теория дифракции по Кирхгофу

 

В основе волновых представлений о распространении когерентного излучения лежит теория дифракции. Под дифракцией света обычно понимают отклонения от простых законов распространения света, описываемых геометрической оптикой. Дифракцию можно наблюдать, когда на пути распространения света находятся непрозрачные препятствия или когда свет проходит через отверстия в экранах. С дифракцией непосредственно связан физический механизм, обуславливающий перераспределение интенсивности в поперечном сечении пространственно-неоднородных лазерных пучков при их распространении в свободном пространстве. В большинстве случаев при описании дифракции можно не учитывать поляризации световой волны. Поэтому в основу теории дифракции мы положим скалярное уравнение Гельмгольца (1.2.20).

Пусть в пространстве распространяется монохроматическая волна

, (1.2.24)

амплитуда которой Y (x,y,z) удовлетворяет уравнению Гельмгольца (1.2.20). Окружим точку наблюдения Р произвольной поверхностью S (рис. 1.2.1.).

Определим возмущение в точке Р в зависимости от возмущения на границе выделенной области. Воспользуемся для этого известной теоремой Грина

, (1.2.25)

где c - некоторая вспомогательная величина, которая также как и Y имеет непрерывные частные производные первого и второго порядков внутри объема V, ограниченного поверхностью S, и на самой поверхности S. Потребуем также, чтобы функция c удовлетворяла уравнению (1.2.20). Операция в формуле (1.2.25) означает дифференцирование по внутренней нормали к поверхности S. В качестве вспомогательной функции c рассмотрим функцию , где r - расстояние между произвольной точкой объема V и точкой Р (радиус-вектор r будем считать направленным от точки Р, как от начала координат). Функция c представляет собой функцию изменения амплитуды поля точечного источника (т.е. так называемую функцию Грина свободного пространства). Для того чтобы эта функция удовлетворяла условиям теоремы Грина, нужно исключить из области V точку Р, где функция c обращается в бесконечность. С этой целью окружим точку Р сферой бесконечно малого радиуса R и исключим ее из области V. Тогда формула (1.2.25) примет вид

. (1.2.26)

Здесь означает объем V без объема сферы, 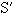- площадь сферы. Поскольку функции Y и c удовлетворяют уравнению Гельмгольца, то объемный интеграл в выражении (1.2.26) равен нулю. Тогда из (1.2.26) следует, что

. (1.2.27)

При выводе соотношения (1.2.27) мы перешли от интегрирования по поверхности 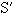к интегрированию по телесному углу W. Таким образом, возмущение в точке Р будет равно

. (1.2.28)

Выражение (1.2.28) известно как дифракционный интеграл Кирхгофа-Гюйгенса.

Дифракционный интеграл (1.2.28) широко используется при решении многих дифракционных задач. Следует, однако, иметь в виду, что возможны и другие математические подходы к анализу дифракции. Они, прежде всего, связаны с выбором другой вспомогательной функции c. В частности, функция c может быть выбрана так, чтобы она обращалась в ноль на поверхности S. Такой подход в какой-то степени упрощает задачу, так как в выражении (1.2.28) обращается в ноль член, содержащий . Однако цена этого упрощения состоит в усложнении функции c.

Для большинства оптических задач выполняется условие

, (1.2.29)

тогда, пренебрегая производной от по сравнению с производной от , формулу (1.2.28) можно записать в виде

. (1.2.30)

Рассмотрим классическую для теории дифракции задачу о прохождении плоской волны через отверстие площадью А в бесконечном непрозрачном экране (рис. 1.2.2). Будем считать, что поверхность, по которой происходит интегрирование, включает экран и бесконечную

полусферу радиуса , ограничивающую пространство справа от экрана. Обозначим координаты точки Р как , , , угол наклона волнового вектора k плоской волны и оси z через g, а угол, задающий направление на точку Р, через a. Из рис. 1.2.2 следует, что

, (1.2.31)

поэтому

(1.2.32)

и

(1.2.33)

С помощью формул (1.2.32) и (1.2.33) интеграл (1.2.30) можно переписать в виде

(1.2.34)

В таком виде этот интеграл известен как формула (интеграл) Френеля-Кирхгофа. В выражении (1.2.34) мы ограничились интегрированием лишь по площади отверстия, считая, что интеграл по бесконечной полусфере обращается в ноль. Последнее утверждение выглядит вполне обоснованным, если предположить, что падающая волна представляет собой очень длинный, но все же конченый цуг волн. Конечный же цуг волн не может достичь бесконечной полусферы за конечное время, тем самым интеграл по поверхности этой полусферы равен нулю.

Более точный математический анализ показывает, что интеграл по бесконечной полусфере стремится к нулю, если выполняется так называемое условие Зоммерфельда, согласно которому

Гораздо боле уязвимым предположением является использованное при получении формулы (1.2.34) второе предположение о равенстве нулю функции Y и ее производной на непрозрачном экране. Дело в том, что равенство нулю решения волнового уравнения и его производной на любом конечном интервале приводит к обращению его в ноль во всем объеме. Однако, несмотря на явный математический изъян, формула (1.2.34) приводит к результатам, хорошо согласующимся с данными экспериментов.

Во многих практических случаях, когда отверстие в экране мало и точка Р располагается вблизи оси, можно считать, что

(1.2.35)

Одновременно, если экран освещается волной, падающей на него перпендикулярно, можно положить, что

. (1.2.36)

Тогда формула (1.2.34) преобразуется в выражение

, (1.2.37)

которое является математическим обобщением принципа Гюйгенса-Френеля. Из него видно, что недостаточно просто предполагать, как это делал в свое время Гюйгенс, что падающая волна выполняет роль источника сферических волн с амплитудами, пропорциональными амплитуде падающей волны в каждой точке. Необходимо потребовать, чтобы фаза вторичного источника отставала от фазы падающей волны на (из-за наличия в правой части (1.2.37) множителя -i).

Поскольку в большинстве практических случаев выполняются соотношения

и , (1.2.38)

можно построить выражение для величины r, ограничиваясь первыми двумя членами ее разложения в ряд Тейлора

(1.2.39)

Используя это выражение, получим следующее приближение для формулы Френеля-Кирхгофа (1.2.34):

. (1.2.40)

Принято говорить о двух случаях применения интеграла (1.2.40): дифракции Френеля и дифракции Фраунгофера. Дифракция Френеля имеет место, когда поле рассчитывается на небольшом расстоянии от отверстия и член , появляющийся в показателе степени экспоненты, следует принимать во внимание. Дифракция же Фраунгофера наблюдается вдали от отверстия, когда этот член пренебрежительно мал.

Вторичные сферические волны, излучаемые каждой точкой в плоскости отверстия, являются в определенном смысле абстракцией и вводятся в приведенном выше подходе к решению дифракционных задач, главным образом, для удобства описания. Более физический подход развит в работах Зоммерфельда. Зоммерфельд рассматривал высказанную еще в 1802 г. Томасом Юнгом идею, заключающуюся в следующем: наблюдаемое поле является суперпозицией падающей волны, прошедшей через отверстие без искажения, и дифрагированной волны, источником которой служит край отверстия. Однако на этом подходе мы подробно останавливаться не будем.