Цель лабораторного занятия

 

Исследование нелинейного уравнения на экстремум методом Зейделя-Гаусса с использования программного пакета Maple.

 

Задание на работу

1. Решить уравнение методом Зейделя-Гаусса вручную (3 итерации).

2. Исследовать уравнение методом Зейделя-Гаусса с помощью программного пакета Maple, вывести график.

3. Сравнить результаты.

 

Описание метода:

Метод Зейделя-Гаусса основан на следующем алгоритме:

1. Дана нулевая точка и функция . Замораживая x0 и подставляя в , рассчитываем y. Тем самым находим точку .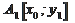

2. Делаем проверку:

3. Если условия не удовлетворяются, то замораживаем y и переходим к п. 1.

Выполнение работы:

1. Расчёт экстремума по методу Зейделя-Гаусса вручную (3 итерации). Дана функция 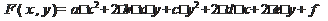 и начальная точка , где Необходимо найти экстремум.

Шаг 1. Определяем точку безусловного экстремума по теореме Ферма:

   

 - точка безусловного экстремума.

Шаг 2.  и замораживаем координату х, т.е решаем уравнение F(x,y) и х=-1.

Берём 1-ю производную от 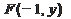 и приравниваем её к 0:

          

Шаг 3. Делаем проверку:

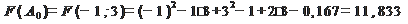
Условия проверки не удовлетворяются, значит, переходим к шагу 2.

Шаг 2.1

 и замораживаем координату у, т.е решаем уравнение F(x,y) и у=-0,5.

Берём 1-ю производную от  и приравниваем её к 0:

          

Шаг 3.1 Делаем проверку:

 Условия проверки не удовлетворяются, значит, переходим к шагу 2.

Шаг 2.2

 и замораживаем координату х, т.е решаем уравнение F(x,y) и х=-0,25.

Берём 1-ю производную от  и приравниваем её к 0:

          

Шаг 3.2 Делаем проверку:

 Условия проверки не удовлетворяются

Окончательный результат получим с помощью программы Maple.

2. На основании алгоритма, описанного выше, составим структурную блок-схему:

Рис. 1

3. Запишем программу в Maple, подставив значения своего варианта (см. Приложение №2).

4. Результат (промежуточный и конечный): корни и число итераций.

5. Отчет о проделанной работе должен содержать:

· Задание на работу

· Ход выполнения работы

· Полученные результаты работы.

· Выводы о проделанной работе

· Сравнительный анализ ручного и программного расчёта в табличной форме:

№ итерации	Программный результат	Расчёт
1	х= у=	х= у=
2	х= у=	х= у=
3	х= у=	х= у=
Безусловный экстремум		х= у=

Лабораторная работа №4

"Синтез системы объекта второго порядка"