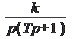Исследование объекта второго порядка с ПИД-регулятором и сравнение с принципом Понтрягина.
Задание на работу
1. Рассчитать настройки регулятора методом Зиглера-Николса для объекта 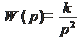 .
.
2. Снять переходную характеристику и сравнить её с переходной характеристикой л.р. 4.
Выполнение работы:
1. Для снятия переходной характеристики объекта составляем структурную схему моделирования в программе 20sim.

Рис. 1
2. Вызовем окно проведения эксперимента, нажав Simulation. Подготовим эксперимент, задав коэффициенты модели объекта, начальные условия, параметры решения и список графиков, выводимых на экран.


Рис. 2 – параметры эксперимента
3. Результат эксперимента необходимо аппроксимировать.
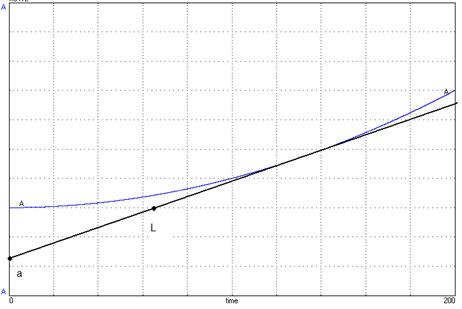
Рис. 3 – результат эксперимента с аппроксимацией
Графически определяем коэффициенты L=6,4 и a=5,1. Исходя из полученных коэффициентов находим настроечные параметры для ПИД-регулятора по методу Зиглера-Николса:

4. Построим структурную схему моделирования одноконтурной системы регулирования с ПИД-законом регулирования.

Рис. 4 – структурная схема с ПИД-законом регулирования
5. Вызовем окно проведения эксперимента, нажав Simulation. Подготовим эксперимент, задав коэффициенты модели объекта, начальные условия, параметры решения и список графиков, выводимых на экран.


Рис. 5 - параметры эксперимента
6. Результат эксперимента:

Рис. 6 – результат эксперимента
7. Отчет должен содержать:
· Цель работы
· Порядок выполнения работы
· Полученные результаты работы
· Выводы о проделанной работе
· Сравнительный анализ с л.р. №4.
Приложение 1. Варианты заданий №1.
| № | Уравнения | № | Уравнения |
| 1/27 | 1) 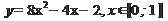 2)
2) 
| 14/40 | 1)  2)
2) 
|
| 2/28 | 1)  2)
2) 
| 15/41 | 1) 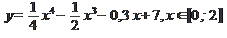 2)
2) 
|
| 3/29 | 1)  2)
2) 
| 16/42 | 1)  2)
2) 
|
| 4/30 | 1)  2)
2) 
| 17/43 | 1)  2)
2) 
|
| 5/31 | 1)  2)
2) 
| 18/44 | 1)  2)
2) 
|
| 6/32 | 1) 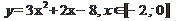 2)
2) 
| 19/45 | 1)  2)
2) 
|
| 7/33 | 1)  2)
2) 
| 20/46 | 1)  2)
2) 
|
| 8/34 | 1)  2)
2) 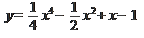
| 21/47 | 1)  2)
2) 
|
| 9/35 | 1)  2)
2) 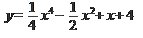
| 22/48 | 1)  2)
2) 
|
| 10/36 | 1)  2)
2) 
| 23/49 | 1) 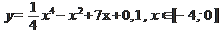 2)
2) 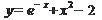
|
| 11/37 | 1)  2)
2) 
| 24/50 | 1)  2)
2) 
|
| 12/38 | 1)  2)
2) 
| 25/51 | 1)  2)
2) 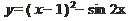
|
| 13/39 | 1)  2)
2) 
| 26/52 | 

|
Приложение 2. Варианты заданий №2.
| № | a | b | c | d | e | f | 
| 
|
| 1 | 1.0 | 1.0 | 2.0 | 0.5 | 0.5 | 0.1 | 3.0 | 3.0 |
| 2 | 2.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0.5 | 0.5 | 4.0 |
| 3 | 1.0 | 0.5 | 1.0 | 1.0 | 0.5 | 0.7 | 3.0 | 1.0 |
| 4 | 1.0 | 0.5 | 1.0 | 0.5 | 1.0 | 0.667 | -3.0 | -0.5 |
| 5 | 1.0 | 0.5 | 1.0 | 1.0 | 1.0 | 0.667 | -0.5 | -3.0 |
| 6 | 1.0 | 0.5 | 2.0 | 0.5 | 0.5 | 0.265 | 1.0 | 4.0 |
| 7 | 1.0 | 0.5 | 2.0 | 0.5 | 1.0 | 0.388 | 3.0 | -1.0 |
| 8 | 1.0 | 0.5 | 2.0 | 1.0 | 0.5 | 0.5 | 0.0 | -4.0 |
| 9 | 1.0 | 0.5 | 2.0 | 1.0 | 1.0 | 1.0 | -0.5 | 4.0 |
| 10 | 1.0 | 1.0 | 2.0 | 0.5 | 0.0 | 0.15 | 1.0 | 5.0 |
| 11 | 1.0 | 1.0 | 2.0 | 0.0 | 0.5 | 0.15 | 0.5 | 4.0 |
| 12 | 1.0 | 1.0 | 2.0 | 0.5 | 1.0 | 0.25 | 0.5 | 3.0 |
| 13 | 1.0 | 1.0 | 2.0 | 1.0 | 0.5 | 0.25 | -1.5 | -3.0 |
| 14 | 1.0 | 1.0 | 2.0 | 1.0 | 1.0 | 0.5 | -1.2 | 4.0 |
| 15 | 1.0 | 1.0 | 2.0 | 1.0 | 0.0 | 1.0 | 2.0 | 2.0 |
| 16 | 1.0 | 1.0 | 2.0 | 0.0 | 1.0 | 0.3 | 0.0 | 3.0 |
| 17 | 1.0 | 0.5 | 2.0 | 0.5 | 0.0 | 0.143 | -0.7 | 3.5 |
| 18 | 1.0 | 0.5 | 2.0 | 0.0 | 0.5 | 0.071 | -0.5 | 4.0 |
| 19 | 1.0 | 0.5 | 2.0 | 1.0 | 0.0 | 0.143 | -1.0 | 3.6 |
| 20 | 1.0 | 0.5 | 2.0 | 0.0 | 1.0 | 0.286 | 0.1 | 4.2 |
| 21 | 1.0 | 0.5 | 1.0 | 0.5 | 0.0 | 0.167 | -1.0 | 3.0 |
| 22 | 1.0 | 0.5 | 1.0 | 0.0 | 0.5 | 0.167 | 1.0 | -3.0 |
| 23 | 1.0 | 0.5 | 1.0 | 1.0 | 0.0 | 1.0 | -1.0 | 4.3 |
| 24 | 1.0 | 0.5 | 1.0 | 0.0 | 1.0 | 0.333 | 0.5 | 2.5 |
| 25 | 2.0 | 0.5 | 1.0 | 0.5 | 0.0 | 0.071 | -1.0 | 4.0 |
| 26 | 2.0 | 0.5 | 1.0 | 0.0 | 0.5 | 0.1 | -0.5 | 3.5 |
| 27 | 2.0 | 0.5 | 1.0 | 1.0 | 0.0 | 0.2 | 3.0 | 1.5 |
| 28 | 2.0 | 0.5 | 1.0 | 0.0 | 1.0 | 0.5 | 0.0 | 3.0 |
| 29 | 2.0 | 0.5 | 1.0 | 0.5 | 0.5 | 0.15 | -0.5 | 3.0 |
| 30 | 2.0 | 1.0 | 1.0 | 0.5 | 0.0 | 0.05 | -0.6 | -4.0 |
| 31 | 2.0 | 1.0 | 1.0 | 0.0 | 0.5 | 0.15 | 0.6 | 2.0 |
| 32 | 2.0 | 1.0 | 1.0 | 0.5 | 0.5 | 0.05 | -0.1 | 4.0 |
| 33 | 2.0 | 0.5 | 1.0 | 1.0 | 1.0 | 0.8 | 3.0 | 1.0 |
| 34 | 2.0 | 1.0 | 1.0 | 1.0 | 0.0 | 0.75 | -4.0 | 0.6 |
| 35 | 2.0 | 1.0 | 1.0 | 0.0 | 1.0 | 1.0 | 0.5 | 3.0 |
| 36 | 2.0 | 1.0 | 1.0 | 1.0 | 0.5 | 0.2 | 0.0 | 5.0 |
| 37 | 2.0 | 1.0 | 2.0 | 0.5 | 0.0 | 0.1 | -4.0 | -0.1 |
| 38 | 2.0 | 1.0 | 2.0 | 0.0 | 0.5 | 0.1 | -4.0 | 0.1 |
| 39 | 2.0 | 1.0 | 2.0 | 0.5 | 0.5 | 0.1 | -3.0 | 0.0 |
| 40 | 2.0 | 1.0 | 2.0 | 1.0 | 0.0 | 0.267 | -1.0 | -3.0 |
| 41 | 2.0 | 1.0 | 2.0 | 0.0 | 1.0 | 0.267 | -1.0 | -3.0 |
| 42 | 2.0 | 1.0 | 2.0 | 0.5 | 1.0 | 0.25 | 4.0 | 1.0 |
| 43 | 2.0 | 1.0 | 2.0 | 1.0 | 0.5 | 0.25 | 3.5 | -1.0 |
| 44 | 2.0 | 0.5 | 1.0 | 0.5 | 1.0 | 0.35 | -0.3 | 2.5 |
| 45 | 2.0 | 0.5 | 1.0 | 1.0 | 0.5 | 0.4 | 3.0 | 1.0 |
| 46 | 2.0 | 1.0 | 1.0 | 0.5 | 1.0 | 0.45 | 0.1 | 1.0 |
| 47 | 1.0 | 2.0 | 2.0 | 0.0 | 1.0 | 0.15 | 1.0 | 2.0 |
| 48 | 1.0 | 2.0 | 2.0 | 1.0 | 1.0 | 0.1 | 1.0 | 1.0 |
| 49 | 1.0 | 2.0 | 2.0 | 2.0 | 2.0 | 0.5 | -2.0 | 2.0 |
| 50 | 1.0 | 1.0 | 1.0 | 2.0 | 2.0 | 0.6 | -4.0 | 2.0 |
Приложение 3. Варианты заданий №3.
| № | W(p) | k | 
| 
|
| 1 |
| 0,5 | 1 |
|
| 2 | 1 | 1 | ||
| 3 | 1 | 10 | ||
| 4 | 2 | 5 | ||
| 5 | 2,5 | 10 | ||
| 6 | 3 | 10 | ||
| 7 | 3,5 | 15 | ||
| 8 | 4 | 10 | ||
| 9 | 4,5 | 1 | ||
| 10 | 5 | 10 | ||
| 11 |
| 1 | 15 | 10 |
| 12 | 1 | 20 | 10 | |
| 13 | 0,1 | 25 | 15 | |
| 14 | 5 | 5 | 10 | |
| 15 | 5 | 10 | 25 | |
| 16 |
| 3 | 5 |
|
| 17 | 3,5 | 7 | ||
| 18 | 3 | 10 | ||
| 19 | 1 | 5 | ||
| 20 | 1 | 5,5 | ||
| 21 |
| 3 | 10 | 15 |
| 22 | 2 | 1 | 0,5 | |
| 23 | 12 | 1 | 10 | |
| 24 | 4 | 10 | 5 | |
| 25 | 4 | 15,5 | 10 | |
| 26 | 2,5 | 12 | 2 | |
| 27 | 3,5 | 5 | 10 | |
| 28 | 4 | 10 | 1,5 | |
| 29 | 4,5 | 12,5 | 1 | |
| 30 | 1 | 10 | 10 | |
| 31 |
| 4 | 1 |
|
| 32 | 1 | 15 | ||
| 33 | 2 | 10 | ||
| 34 | 2,5 | 5 | ||
| 35 | 3 | 3 | ||
| 36 | 3,5 | 4 | ||
| 37 | 4 | 25 | ||
| 38 | 4,5 | 5,5 | ||
| 39 | 5 | 6,5 | ||
| 40 | 2 | 4 |

 |
 2018-02-13
2018-02-13 201
201