1.1. ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
При рассмотрении объектов управления указывалось, что их состояние равновесия может быть устойчивым неустойчивым и нейтральным. То же можно сказать и о системах автоматического регулирования.
Неустойчивый объект может входить в устойчивую систему автоматического регулирования. В этом случае речь идет о системах с искусственной устойчивостью. Однако неустойчивые линейные системы автоматического регулирования сами по себе без дополнительных устройств искусственной устойчивости не могут быть применены на практике. Поэтому первым условием работоспособности линейной системы автоматического регулирования является ее устойчивость.
Необходимым и достаточным условием устойчивости линейного звена является отрицательное значение вещественной части всех полюсов передаточной функции этого звена.
Для разомкнутой системы регулирования согласно передаточной функции:
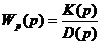 , , | 1.1 |
где К(р) и D(р) — алгебраические полиномы от р. Условием устойчивости разомкнутой системы является отрицательный знак вещественной части корней характеристического уравнения:
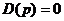 , , | 1.2 |
Для суждения об устойчивости замкнутой системы в качестве передаточной функции можно рассматривать любую функцию, связывающих сигналы на входе и выходе системы.
Рассмотрим в качестве передаточной функции замкнутой системы передаточную функцию по регулируемой величине:
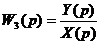 = = 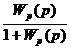 , , | 1.3 |
Подставив выражение Wp(p) из (1.1), получим:
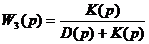 , , | 1.4 |
Выражение любой другой передаточной функции замкнутой системы отличается от (1.4) только числителем. Знаменатель для всех функций замкнутой системы остается тем же. Вводя общее обозначение передаточной функции замкнутой системы:
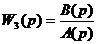 , , | 1.5 |
во всех случаях для знаменателя замкнутой системы будем иметь:
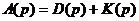 , , | 1.6 |
Условием устойчивости замкнутой системы является отрицательный знак вещественной части всех корней характеристического уравнения:
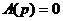 , , | 1.7 |
Это условие устойчивости, доказанное для линейных систем, было распространено на линеаризованные уравнения нелинейных систем А. М. Ляпуновым в 1892 г.
Исследование устойчивости сводится, таким образом, к определению знаков вещественной части корней характеристического уравнения, т. е. к вопросу распределения корней относительно мнимой оси в комплексной плоскости р.
Уравнения степени не выше 4-й могут быть решены, так как для них существуют аналитические выражения, определяющие их корни. Для уравнений более высокой степени (степени 5-й и выше) таких выражений нет. Но для суждения об устойчивости нет необходимости знать значение корней, достаточно лишь иметь суждение о знаке их вещественной части.
Существенным является поэтому выяснение правил, которые позволили бы, минуя вычисление самих корней, ответить на вопрос: как распределены корни в комплексной плоскости относительно мнимой оси. Правила, позволяющие определить расположение корней относительно мнимой оси, называются критериями устойчивости.
Существует несколько критериев устойчивости. Все они математически эквивалентны, так как решают вопрос — лежат ли все корни характеристического уравнения в левой полуплоскости или нет. Практическое использование того или иного критерия для конкретной задачи решается характером самой задачи.
В настоящее время при решении вопроса об устойчивости используются следующие критерии: алгебраические —а) Рауса, б) Гурвица; частотные —а) Михайлова, б) Найквиста.
1.2. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
Задача нахождения соотношений между коэффициентами характеристического уравнения линейной системы, обеспечивающих ее устойчивость, давно привлекала внимание инженеров и математиков. Еще в 1860 г. И. А. Вышнеградский, исследуя систему регулирования паровой машины, сформулировал условия, связывающие коэффициенты характеристического уравнения третьей степени, при которых система устойчива. Эта же задача привлекла внимание Дж. Максвелла и А. Стодола. К решению задачи для произвольной степени уравнения были привлечены математики Раус и Гурвиц. Ими были получены решения задачи устойчивости в несколько различных видах.
Раус опубликовал свое решение в 1875 г. в виде получившей известность таблицы Рауса. Гурвицем был опубликован критерий устойчивости в 1895 г. в виде системы определителей. Оба эти критерия приводят к одним и тем же алгебраическим неравенствам и по существу отличаются только общей формой получения их. Поэтому эти критерии часто объединяют, называя критерием Рауса — Гурвица.
Опуская доказательство каждого из этих критериев, приведем их математическую формулировку и покажем примеры их применения.
Критерий Рауса. Пусть дано характеристическое уравнение системы:
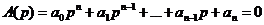 | 1.8 |
Составим табл. 1.1 называемую таблицей Рауса.
Таблица 1.1
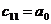 | 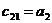 |  | 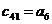 | |
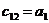 | 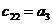 | 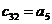 | 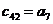 | |
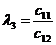 | 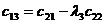 | 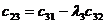 | 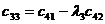 | 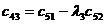 |
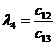 | 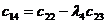 | 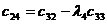 | 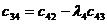 | 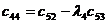 |
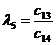 | 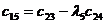 | 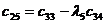 | 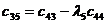 | 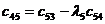 |
Правило составления таблицы легко усмотреть из ее построения. Любой из коэффициентов таблицы Рауса cki при 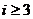 (k обозначает номер столбца, a i — номер строки таблицы) можно найти по формуле:
(k обозначает номер столбца, a i — номер строки таблицы) можно найти по формуле:
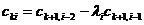 , , | 1.9 |
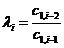 , при , при 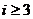 |
Число строк таблицы Рауса равно степени уравнения плюс единица,
т. е. (n +1). Коэффициентам с отрицательными индексами соответствуют нули. Критерий устойчивости Рауса формулируется следующим образом. Для того чтобы система была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительны, т. е.
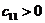 ; ; 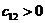 ; ; 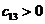 ; ; 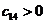 ,…, ,…, 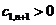 | 1.10 |
При составлении таблицы Рауса для численно заданных коэффициентов уравнения можно в целях упрощения вычислений умножать или делить строки таблицы на положительную величину. Это не меняет результат.
Если не все коэффициенты первого столбца положительны, т. е. система неустойчива, то число корней уравнения, лежащих в правой полуплоскости, равно числу перемен знаков в первом столбце таблицы.
Пример 1.1. Пусть
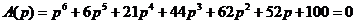
Требуется определить количество корней, лежащих в правой полуплоскости.
Составим таблицу Рауса (табл. 1.2). Как видно из таблицы, в первом столбце имеют место две перемены знака: с плюса на минус и с минуса на плюс. Следовательно, рассматриваемое характеристическое уравнение имеет два корня в правой полуплоскости и соответствует неустойчивой системе.
К р и т е р и й Г у р в и ц а. Пусть дано характеристическое уравнение системы (1.8).Составим таблицу коэффициентов, называемую таблицей Гурвица.

Таблица 1.2
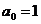 | 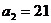 | 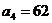 | 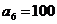 | |
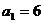 | 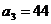 | 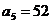 | 0 | |
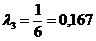 | 21-0,167·44=13,65 | 62-0,167·52=53,3 | 100-0,167·0=100 | 0 |
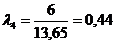 | 44-0,44·53,3=20,6 | 52-0,44·100=8 | 0-0,44·0=0 | 0 |
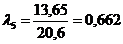 | 53,3-0,662·8=48,0 | 100-0,622·0=100 | 0 | 0 |
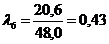 | 8-0,43·100= - 35,0 | 0 | 0 | 0 |
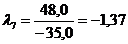 | 100-1,37·0=100 | 0 | 0 | 0 |
Правило составления таблицы видно из ее построения. Первая строка образуется из коэффициентов уравнения с индексами 0, 2, 4, и т. д. Вторая строка — из коэффициентов уравнения с индексами 1, 3, 5, и т. д. Каждая последующая строка образуется коэффициентами уравнения с индексами на единицу больше индексов коэффициентов предшествующей строки; при этом коэффициенты с индексами меньше нуля и больше n заменяются нулями. Таблица содержит п строк, где п — степень уравнения.
Из таблицы Гурвица составляются определители k -го порядка Δ k отчеркиванием в таблице k строк и k столбцов:
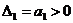 ;
; 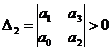 ;
;
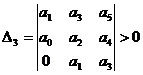 и т. д. и т. д. | 1.11 |
эти определители называются определителями Гурвица.
Критерий устойчивости Гурвица формулируется следующим образом. Система устойчива, если 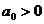 и все определили Гурвица больше нуля, т. е.
и все определили Гурвица больше нуля, т. е.
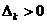 , где
, где 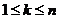 .
.
Рассмотрим более подробно случаи, когда n = 1,…,4
1) n = 1,
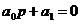 , , | 1.12 |
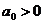 ;
; 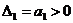 ;
;
2) n = 2,
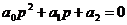 , , |
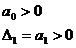 ; ; 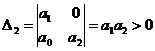 , , | 1.13 |
Последнее условие, при наличии предшествующего, эквивалентно условию 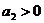 .
.
Таким образом, условия устойчивости для уравнения второй степени сводятся к требованиям:
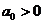 , , 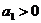 , , 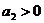 ; ; | 1.14 |
3) n = 3
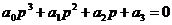 , , |
Условия устойчивости:
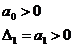 ;
;
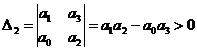 ;
;
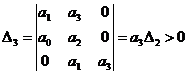 ,
,
Последнее условие, при наличии предшествующего, эквивалентно условию 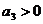 .
.
Условие 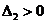 при
при 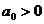 ;
; 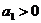 ;
; 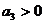 возможно лишь при
возможно лишь при 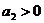 .
.
Таким образом, условия устойчивости для уравнения третьей степени сводятся к требованиям:
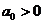 , , 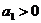 , , 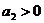 , , 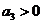 , , | 1.15 |
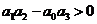 ; ; | 1.16 |
4) n = 4,
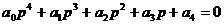 ,
,
Условия устойчивости:
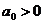 ;
; 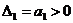 ;
;
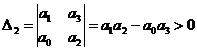 ;
;
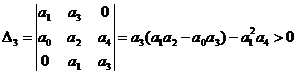 ;
;
Последнее условие, при наличии предшествующего, эквивалентно условию 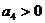 .
.
Условие 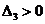 при
при 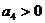 возможно только при
возможно только при 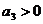 и
и 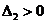 . Условие
. Условие 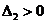 при
при 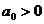 ,
, 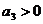 и
и 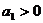 возможно при
возможно при 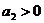 .
.
Таким образом, условия устойчивости для уравнения четвертой степени сводятся к требованиям:
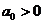 , , 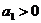 , , 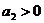 , , 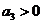 , , 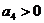 , , | 1.17 |
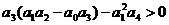 ; ; | 1.18 |
Из сказанного следует, что условия устойчивости для уравнений первой и второй степени сводятся к требованию положительности коэффициентов характеристического уравнения.
Для уравнений третьей и четвертой степени, помимо положительности коэффициентов характеристического уравнения, необходимо соблюдение неравенств (1.16) и (1.18).
При 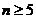 число подобных дополнительных неравенств возрастает, поэтому критерий устойчивости Гурийца рационально использовать при
число подобных дополнительных неравенств возрастает, поэтому критерий устойчивости Гурийца рационально использовать при 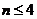 .
.
Из структуры построения определителей Гурвица следует, что:
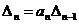 , , | 1.19 |
Согласно критерию устойчивости Гурвица, система устойчива, если все определители Гурвица больше нуля и, в частности, 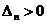 .
.
Система находится на границе устойчивости, когда:
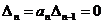 , , | 1.20 |
Это равенство возможно в двух случаях: 1) 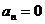 и 2)
и 2) 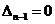 .
.
В первом случае говорят, что система находится на границе апериодической устойчивости (один из корней характеристического уравнения равен нулю).
Во втором случае говорят, что система находится на границе колебательной устойчивости (два сопряженных корня характеристического уравнения находятся на мнимой оси).
В большинстве случаев 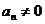 и, следовательно, если система находится на границе устойчивости, то это граница колебательной устойчивости.
и, следовательно, если система находится на границе устойчивости, то это граница колебательной устойчивости.
Пример 1.2. Пусть дано характеристическое уравнение:
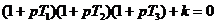 , , | 1.21 |
Это уравнение соответствует системе регулирования, содержащей три инерционных звена с постоянными времени 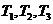 и общим коэффициентом усиления k. Необходимо найти предельное значение k, при котором система перестает быть устойчивой, т. е. kпр как функцию Тi, i = 1, 2, 3.
и общим коэффициентом усиления k. Необходимо найти предельное значение k, при котором система перестает быть устойчивой, т. е. kпр как функцию Тi, i = 1, 2, 3.
Перепишем уравнение в виде:
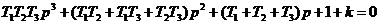
Согласно критерию устойчивости Гурвица, система устойчива, если выполняются неравенства (1.15) и (1.16), т.е. если все коэффициенты уравнения положительны и выполняется неравенство:
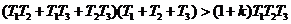 , , | 1.22 |
Положительный знак коэффициентов вытекает из условия задачи. Неравенство (1.22) может быть переписано в виде:
 , , | 1.23 |
где
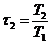 ;
; 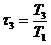 ;
;
Из полученного неравенства видно, что оно нарушается при:
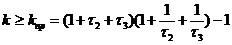 , , | 1.24 |
Из (1.24) следует, что предельный коэффициент усиления kпр системы определяется не абсолютной величиной постоянных времени звеньев, а их относительным значением и kпр тем больше, чем больше величины 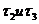 т. е. чем более резко отличаются постоянные времени друг от друга. В частном случае, когда
т. е. чем более резко отличаются постоянные времени друг от друга. В частном случае, когда 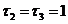 , т. е.
, т. е. 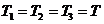 , значение kпр минимально и равно всего лишь 8.
, значение kпр минимально и равно всего лишь 8.
1.3. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
П р и н ц и п а р г у м е н т а. В основе частотных критериев устойчивости лежит известный в теории функций комплексного переменного принцип аргумента.
Пусть дано алгебраическое уравнение с действительными коэффициентами:
 , , | 1.25 |
Многочлен А(р) можно представить в виде:
 , , | 1.26 |
где pi — корни уравнения А(р) = 0.
Положим 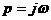 , тогда:
, тогда:
 , , | 1.27 |
Рассмотрим геометрическое представление комплексного числа 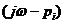 на комплексной плоскости р. Начало вектора, изображающего это комплексное число, лежит в точке pi, а конец — на мнимой оси в точке
на комплексной плоскости р. Начало вектора, изображающего это комплексное число, лежит в точке pi, а конец — на мнимой оси в точке 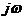 (рис. 1.1)
(рис. 1.1)
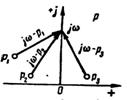 | Рис. 1.1 |
Найдем аргумент комплексного числа:
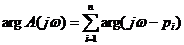 , , | 1.28 |
При изменении аргумента A (jω) с изменением ω в пределах от —∞ до +∞:
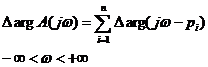 , , | 1.29 |
Согласно (1.29), для подсчета изменения аргумента необходимо подсчитать сумму изменений аргументов выражений вида 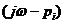 . Это изменение аргумента зависит от того, в какой (правой или в левей) полуплоскости лежит корень pi. Рассмотрим эти два случая.
. Это изменение аргумента зависит от того, в какой (правой или в левей) полуплоскости лежит корень pi. Рассмотрим эти два случая.
Корень pi, лежит в левой полуплоскости (рис. 1.2, а). При изменении ω в пределах от — ∞ до + ∞ конец вектора 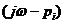 скользит вдоль мнимой оси снизу вверх, поворачиваясь против часовой стрелки на 180°, и, следовательно, изменение аргумента при этом:
скользит вдоль мнимой оси снизу вверх, поворачиваясь против часовой стрелки на 180°, и, следовательно, изменение аргумента при этом:
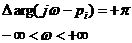 , , | 1.30 |
Корень pi, лежит в правой полуплоскости (рис. 1.2,6). В этом случае, рассуждая аналогично, получим:
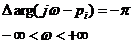 , , | 1.31 |
Допустим, что уравнение А(р) = 0 имеет m корней в правой полуплоскости и l корней в левой полуплоскости. При этом l + m = n.
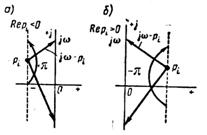 | Рис. 1.2 |
Тогда, на основании (1.27), (1.30) и (1.31):
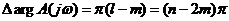 , , | 1.32 |
Уравнение (7.32) представляет собой выражение принципа аргумента, который формулируется следующим образом, Изменение аргумента A (jω) при изменении ω от — ∞ до + ∞ равно разности между числом корней l (уравнения А (р) = 0), лежащих в левой полуплоскости, и числом корней т, лежащих в правой полуплоскости, умноженной на π.
К р и т е р и й М и х а й л о в а. Критерий устойчивости
А. В. Михайлова, сформулированный им в 1938 г.,является по существу геометрической интерпретацией принципа аргумента. Пусть дано характеристическое уравнение системы (1.8):
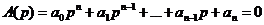 , , | 1.33 |
Полином А(р) в этом случае называется характеристическим полиномом. Для того чтобы система была устойчива, необходимо, чтобы все корни характеристического уравнения лежали в левой полуплоскости, т. е. чтобы т = 0. В этом случае согласно (1.32) должно удовлетворяться уравнение:
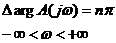 , , | 1.34 |
Из условия (1.34) следует, что все корни уравнения А(р)=0 лежат в левой полуплоскости.
Геометрическое место конца вектора A (jω) при 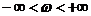 называется годографом вектора A(jω), или годографом Михайлова. Согласно (1.33), уравнение годографа Михайлова:
называется годографом вектора A(jω), или годографом Михайлова. Согласно (1.33), уравнение годографа Михайлова:
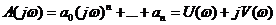 , , | 1.35 |
где действительная и мнимая части комплекса соответственно будут:
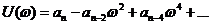 , , | 1.36 |
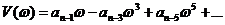 , , | 1.37 |
Из (1.36) и (1.37) следует, что действительная часть является четной функцией ω:
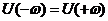 , , | 1.38 |
а мнимая часть A (jω) является нечетной функцией ω:
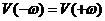 , , | 1.39 |
Следовательно,
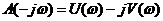 , , | 1.40 |
т.е. A (jω)и A (-jω) являются сопряженными комплексными величинами и, таким образом,
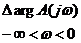 = = 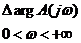 | 1.41 |
Учитывая (1.41), уравнение можно записать в виде:
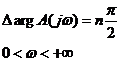 , , | 1.42 |
 | Рис. 1.3 |
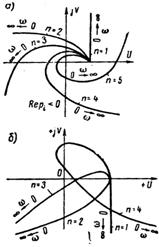
Из (1.42) следует формулировка критерия устойчивости Михайлова. Система автоматического регулирования устойчива, если при изменении ω от 0 до + ∞ вектор А (jω) поворачивается на угол 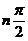 где n — степень характеристического уравнения А (р) = 0; или, иначе, если годограф A(jω) с ростом ω от 0 до + ∞, начинаясь на действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) п квадрантов.
где n — степень характеристического уравнения А (р) = 0; или, иначе, если годограф A(jω) с ростом ω от 0 до + ∞, начинаясь на действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) п квадрантов.
На рис.1.3.а показаны годографы А (jω) устойчивых систем для разных значений п. Все они охватывают соответствующее число квадрантов в положительном направлении.
На рис.1.3.б показаны годографы неустойчивых систем. Все они не удовлетворяют условию обхода п квадрантов в положительном направлении.
Годограф А (jω) можно построить по уравнениям (1.36) и (1.37), задаваясь значениями ω и вычисляя U и V.
Годограф можно также построить геометрически исходя из выражения (1.35). Вектор А (jω) при этом представляет собой замыкающую многоугольника, стороны которого равны соответственно 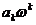 и образуют между собой угол в 90°. На рис. 1.4 это построение показано для одной точки ω = ω 1, когда:
и образуют между собой угол в 90°. На рис. 1.4 это построение показано для одной точки ω = ω 1, когда:
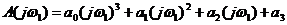 , , | 1.43 |
Задаваясь значениями ω в пределах нуль — бесконечность, строят подобным образом весь годограф.
Согласно уравнению (1.6) характеристический полином замкнутой системы можно представить в виде суммы К(р) и D(p). Годографы D(jω) и K(jω) могут быть представлены в виде произведения более простых годографов, которые обычно известны и для типовых звеньев имеют простой вид. Отсюда следует, что для построения годографа А (jω) необходимо построить годограф D(jω), построить годограф K(jω), сложить векторы D(jω) и K(jω) для каждого значения ω.
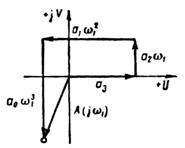 | Рис. 1.4 |
В случае, когда K(jω) = k, т. е. не зависит от частоты ω, построение упрощается. Последние две операции заменяются простым смещением годографа D(jω) вправо вдоль вещественной оси на величину k или, что то же самое, смещением мнимой оси влево на величину k.
Пример 7.3. Определить предельный коэффициент усиления k пр системы автоматической стабилизации напряжения генератора.
Передаточная функция разомкнутой системы имеет вид:
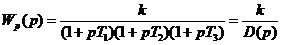 , , |
где k = k1 k2 k3.
Характеристическое уравнение замкнутой системы:
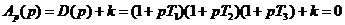 , , |
Для решения задачи следует построить годограф Михайлова:
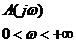 = = 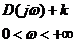 |
Для этого построим вначале годограф:
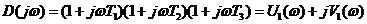 , , |
Пусть T1 = 2,0 сек, T2 = 0,5 сек, T3 = 0,1 сек.
Тогда:
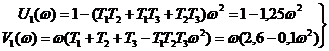 , , | 1.44 |
и годограф D(jω) имеет вид, показанный па рис. 1.5.
Для того чтобы получить годограф А (jω) достаточно мнимую ось сместить влево на величину k. Из рис. 1.5 следует, что система будет на границе устойчивости, если k будет равно kпр, при котором годограф А(jω) пройдет через начало координат. Величина knp, как это видно из рис. 1.5, может быть определена из уравнений:
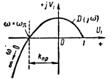 | Рис. 1.5 |
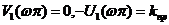 , , | 1.44` |
где ω — частота пересечения, т. е. частота, соответствующая точке пересечения годографа D (jω) с действительной осью.
Решая уравнения (1.44)и (1.44'), для ω = ωπ получим:
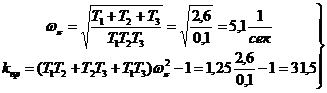 , , | 1.45 |
Легко заметить, что при подстановке выражений ωπ, τ2, τ3 формулы (1.45) и (1.24) совпадают.
К р и т е р и й Н а й к в и с т а. Для исследования устойчивости усилителей с обратной связью Найквист в 1932 г. предложил критерий устойчивости, основанный на исследовании частотных характеристик системы. Этот критерий был по-новому обоснован, обобщен и применен в теории автоматического регулирования А. В. Михайловым в 1938 г. Для исследования устойчивости замкнутой системы регулирования согласно этому критерию необходимо знать частотный годограф разомкнутой системы. Эту характеристику можно получить как аналитически, так и экспериментально. Последнее обстоятельство выгодно отличает рассматриваемый критерий устойчивости от ранее изложенных.
Критерий устойчивости Найквиста имеет ясный физический смысл. Он связывает стационарные частотные свойства разомкнутой системы с нестационарными свойствами замкнутой системы.
Критерий устойчивости, основанный на построении частотного годографа разомкнутой системы. Пусть передаточная функция разомкнутой системы регулирования:
 , , |
Образуем функцию:
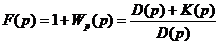 , , | 1.46 |
Числитель этой функции представляет собой характеристический полином замкнутой системы, знаменатель — характеристический полином разомкнутой системы. Пусть степень D(p) равна n и степень K(p) равна r. Из физических соображений следует, что:
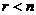 , , | 1.47 |
В противном случае, при 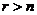 из передаточной функции W(р) можно выделить слагаемые с р выше нулевой степени, что соответствует дифференцирующим звеньям, которые, как было указано в гл. III, не могут быть реализованы на практике. I
из передаточной функции W(р) можно выделить слагаемые с р выше нулевой степени, что соответствует дифференцирующим звеньям, которые, как было указано в гл. III, не могут быть реализованы на практике. I
Учитывая неравенство (1.47),можно утверждать, что степень полинома D(p)+K(p) также равна п.
Рассмотрим два случая состояния разомкнутой системы: устойчива и неустойчива.
1-й случай — система в разомкнутом состоянии устойчива.
Тогда согласно критерию устойчивости Михайлова изменение аргумента характеристического полинома разомкнутой системы:
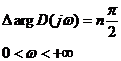 , , |
Если потребовать, чтобы система в замкнутом состоянии была устойчива, то должно удовлетворяться равенство:
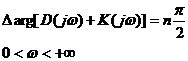 , , |
Из (1.46) при этом следует, что:
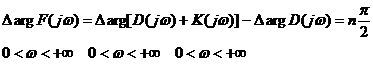 , , | 1.48 |
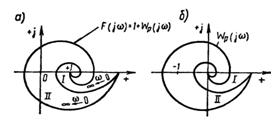
Таким образом, система автоматического регулирования устойчива, если изменение аргумента вектора F(jω) при изменении ω от 0 до ∞, равно нулю.
На рис. 1.6, а показаны два годографа F(jω) = 1 + Wp (jω) соответствует устойчивой системе: он не охватывает точку (0,0), II — неустойчивой: он охватывает точку (0,0).
 | Рис. 1.6 |
Так как F(jω) отличается от Wp (jω) на +1, то сказанное можно сформулировать непосредственно для характеристики Wp (jω) (см. рис. 1.6, б).
Замкнутая система устойчива, если годограф разомкнутой системы Wp (jω) не охватывает точку (—1,j0).
Пример 1.4. Применим критерий Найквиста для определения предельного коэффициента системы регулирования, рассмотренной в примере 1.3 для которой:
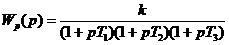 , , |
Частотные годографы для этой системы при разных значениях k показаны на рис. 1.7. Согласно критерию Найквиста, при k = k1 система устойчива, при k = k2 — неустойчива.
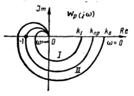 | Рис. 1.7 |
Для определения значения k пр необходимо найти значение k, при котором годограф проходит через точку (—1,j0), т. е. решить уравнение:
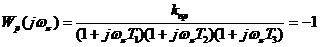 ,
,
или
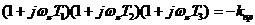
Составив уравнения для мнимых и действительных частей этого уравнения, находим ωπ и kпр:
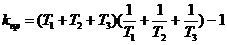
Полученное решение совпадает с формулами (1.45) и (1.24), найденными с помощью критериев Михайлова и Гурвица.
2-й случай — система в разомкнутом состоянии неустойчива.
При рассмотрении многоконтурных и одноконтурных систем, содержащих неустойчивые звенья, разомкнутая система может оказаться неустойчивой.
Пусть система в разомкнутом состоянии неустойчива, при этом характеристическое уравнение разомкнутой системы имеет m корней в правой полуплоскости. Тогда согласно принципу аргумента (1.32):
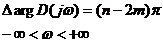 , , |
или, учитывая симметрию характеристик для + ω и – ω,
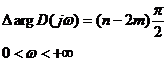 , , |
Если потребовать, чтобы система в замкнутом состоянии была устойчива, то должно выполняться равенство:
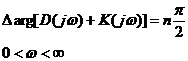 , , |
При этом [согласно (1.46)]:
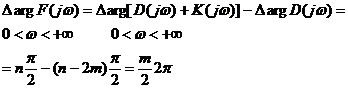 , , | 1.49 |
Таким образом, система автоматического регулирования устойчива, если при изменении ω от нуля до бесконечности годограф разомкнутой системы Wp (jω) охватывает m/2 раз точку (—1; j0) в положительном направлении, где т — число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.
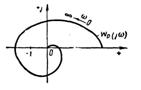 | Рис. 1.8 |
Кратность охвата может быть наглядно определена числом оборотов, совершенных вектором, проведенным из точки (—1;j0) в текущую точку годографа.
На рис. 1.8показан годограф устойчивой системы в замкнутом состоянии, которая в разомкнутом состоянии неустойчива, а число корней ее т = 2. Годограф охватывает в положительном направлении точку (—1, j0) один раз (m/2 =1) следовательно, согласно (1.49) система в замкнутом состоянии устойчива.
2. ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К КОНТРОЛЬНЫМ РАБОТАМ
2.1 ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
В заданиях приводится 31 вариант исходных данных. Номер варианта семестровой работы определяется номером списка группы.
Семестровое задание выполняется в сроки, предусмотренные учебным планом, и рабочей программой (методикой рейтингового контроля). Если работа правильно оформлена и ее содержание адекватно отвечает вопросам задания, то она зачитывается. В противном случае контрольная работа возвращается студенту для доработки с замечаниями преподавателя.
Отчет по контрольной работе выполняется на писчей бумаге формата А4 (297x210) с обязательной нумерацией страниц. Расчетные формулы, соотношения должны иметь сквозную нумерацию в пределах одной контрольной работы. Нумеруются также рисунки, содержащие схемы, графики и другие иллюстрации, и таблицы. Рисунки желательно представлять в карандаше. В конце пояснительной записки следует поместить список использованной литературы.
В пояснительной записке необходимо предусмотреть поля для замечаний преподавателя.
Образец титульного листа контрольной работы:
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО
УНИВЕРСИТЕТА
КАФЕДРА «Технология машиностроительных производств»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине:
«Теория автоматического управления»
Выполнил:
студент группы КТМ-021
Иванов И.И.
Проверил:
преподаватель
Сидоров В.В.
Камышин
2006
2.2 КОНТРОЛЬНАЯ РАБОТА
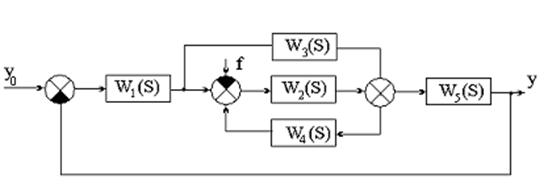
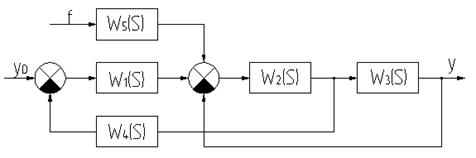
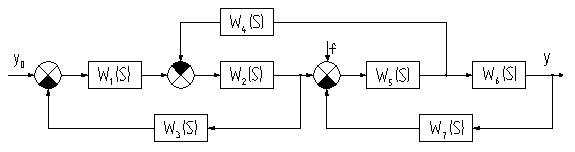
Задана структурная схема системы автоматического регулирования (рис.2).
 |
| Рис. 2 а |
 |
| Рис. 2 б |
 |
| Рис. 2 в |
 |
| Рис. 2 г |
Необходимо:
1) найти все эквивалентные (расчетные) передаточный функции замкнутой системы;
2) для разомкнутой чисти системы определить частотные функции и построить соответствующие частотные характеристики: КЧХ, АЧХ, ФЧХ;
5)исследовать заданным методом устойчивость системы.
Передаточные функции звеньев структурных схем имеют вид:
W1(S)= 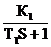 ; ; | W2(S)= 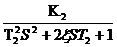 ; ; | W3(S)=К3; |
| W4(S)=К4; | W5(S)= 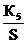 ; ; | W6(S)=К6. |
Варианты числовых значений параметров приведены в табл. 2.1.
Таблица 2.1
| № вар | Значение параметров | № структур-ной схемы | Критерий устойчи-вости | ||||||||
| К1 | К2 | К3 | К4 | К5 | К6 | Т1 | Т2 | ξ | |||
| 1. | 2 | 0.8 | 4 | 0.1 | 2.4 | 0.5 | 0.01 | 0.2 | 0.8 | 2б | Михайлова |
| 2. | 1.5 | 4 | 0.6 | 0.4 | 3 | - | 0.1 | 0.4 | 0.1 | 2а | Гурвица |
| 3. | 1.2 | 3.5 | 3 | 0.06 | 0.18 | 1.2 | 0.08 | 0.1 | 0.1 | 2б | Рауса |
| 4. | 0.8 | 3 | 5 | 0.2 | 0.13 | - | 0.03 | 0.3 | 0.2 | 2в | Найквиста |
| 5. | 1.3 | 5 | 1.1 | 0.15 | 0.1 | - | 0.04 | 0.5 | 1.1 | 2г | Рауса |
| 6. | 0.7 | 6 | 0.09 | 1.5 | 2 | - | 0.2 | 0.12 | 1.4 | 2в | Найквиста |
| 7. | 1.6 | 2 | 0.12 | 0.09 | 1.1 | - | 0.06 | 0.6 | 0.3 | 2г | Гурвица |
| 8. | 2 | 1.8 | 0.15 | 0.8 | 1.8 | 0.9 | 0.035 | 0.15 | 2 | 2б | Гурвица |
| 9. | 7 | 1.3 | 2.8 | 0.12 | 0.7 | - | 0.11 | 0.7 | 2 | 2в | Михайлова |
| 10. | 4 | 2.4 | 0.19 | 0.9 | 3.5 | 4 | 0.3 | 0.3 | 0.6 | 2в | Гурвица |
| 11. | 1.6 | 2.5 | 1.3 | 0.7 | 2.8 | - | 0.07 | 0.9 | 0.7 | 2а | Найквиста |
| 12. | 5 | 1.5 | 3.7 | 0.18 | 1.6 | - | 0.14 | 0.25 | 1 | 2а | Рауса |
| 13. | 1.6 | 3 | 3 | 1.1 | 0.8 | 1.5 | 0.5 | 0.45 | 0.4 | 2б | Рауса |
| 14. | 1.7 | 2 | 3.6 | 0.74 | 0.5 | - | 0.4 | 0.8 | 0.95 | 2г | Михайлова |
| 15. | 1.4 | 6 | 0.8 | 0.4 | 3.2 | - | 0.06 | 0.52 | 1.2 | 2а | Михайлова |
| 16. | 5 | 3.3 | 2.1 | 0.34 | 1.3 | 2.5 | 0.05 | 0.27 | 1.5 | 2б | Михайлова |
| 17. | 2.7 | 4.5 | 2.3 | 0.5 | 3.6 | - | 0.15 | 0.6 | 0.5 | 2а | Гурвица |
| 18. | 3.4 | 1.2 | 4 | 0.21 | 2.6 | - | 0.04 | 0.47 | 1.25 | 2г | Рауса |
| 19. | 2 | 0.8 | 2 | 0.5 | 2.4 | 0.1 | 0.01 | 0.02 | 0.8 | 2б | Михайлова |
| 20. | 1 | 4.5 | 0.6 | 0.2 | 2 | - | 0.2 | 0.3 | 0.1 | 2в | Гурвица |
| 21. | 1.5 | 4 | 2.5 | 0.05 | 0.2 | 1.2 | 0.06 | 0.1 | 0.1 | 2б | Рауса |
| 22. | 0.5 | 2. | 5 | 0.2 | 0.15 | - | 0.03 | 0.3 | 0.2 | 2в | Найквиста |
| 23. | 0.5 | 6 | 0.08 | 1 | 2 | - | 0.2 | 0.12 | 1.4 | 2г | Михайлова |
| 24. | 0.7 | 5 | 0.05 | 0.09 | 1.1 | - | 0.05 | 0.5 | 0.4 | 2г | Гурвица |
| 25. | 3 | 2.5 | 0.2 | 0.9 | 3.5 | 4 | 0.3 | 0.3 | 0.4 | 2в | Гурвица |
| 26. | 1.5 | 2 | 1.3 | 0.7 | 2.9 | - | 0.05 | 0.9 | 0.5 | 2в | Найквиста |
| 27. | 1.5 | 6 | 38 | 0.5 | 0.5 | - | 0.4 | 0.8 | 0.05 | 2г | Михайлова |
| 28. | 5 | 3.5 | 2.5 | 0.5 | 1.5 | 2 | 0.05 | 0.25 | 1.5 | 2б | Найквиста |
| 29. | 2.5 | 4.3 | 2.3 | 0.5 | 3.6 | 4 | 0.15 | 0.6 | 0.5 | 2в | Гурвица |
| 30. | 2.6 | 1.6 | 1.5 | 0.7 | 2.5 | - | 0.07 | 0.8 | 0.7 | 2б | Найквиста |
| 31. | 1.6 | 2 | 3 | 1.5 | 0.8 | 1.5 | 0.5 | 0.45 | 0.5 | 2б | Рауса |
 2018-02-13
2018-02-13 1806
1806