К уравнению с разделяющимися переменными приводятся однородные ДУ первого порядка.
Функция y=φ (x,у) называется однородной функцией n-го порядка, если при умножении каждого ее аргумента на произвольный множитель λ вся функция умножится на λn , т.е.
f (λ . x; λ . y)= λn . f (x, y).
Дифференциальное уравнение y’= f (x, y) называется однородным, если функция f (x, y) есть однородная функция нулевого порядка.
Покажем, что однородное ДУ y’= f (x, y) можно записать в виде
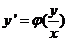
Если f (x, y)- функция нулевого порядка, то, по определению, f (x, y)= f (λ . x; λ . y)
Положив 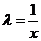 , получаем:
, получаем:
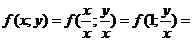
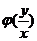
Однородное уравнение 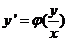 преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки).
преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки).
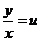 или, что то же самое, y=u
или, что то же самое, y=u  x.
x.
Действительно, подставив y=ux и y’=u’x+u в уравнение 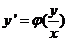 , получаем u’x+u=
, получаем u’x+u= 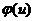 или
или 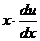 =
= 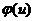 -u, т.е. уравнение с разделяющимися переменными.
-u, т.е. уравнение с разделяющимися переменными.
Найдя его общее решение (или общий интеграл), следует заменить в нем u на 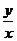 . Получим общее решение (интеграл) исходного уравнения.
. Получим общее решение (интеграл) исходного уравнения.
Однородное уравнение часто задается в дифференциальной форме:
P(x, y) dx + Q(x, y) dy = 0
Оно будет однородным, если P(x, y) и Q(x, y)- однородные функции одинакового порядка.
Переписав уравнение P(x, y) dx + Q(x, y) dy = 0 в виде 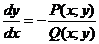 и применив в правой части рассмотренное выше преобразование, получим уравнение
и применив в правой части рассмотренное выше преобразование, получим уравнение 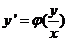 .
.
Линейные уравнения. Уравнения Бернулли.
Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде
y’+p(x)  y=g(x),
y=g(x),
где p(x) и g(x) – заданные функции, в частности – постоянные.
Особенность ДУ y’+p(x)  y=g(x): искомая функция y и ее производная y’ входят в уравнение в первой степени, не перемножаясь между собой.
y=g(x): искомая функция y и ее производная y’ входят в уравнение в первой степени, не перемножаясь между собой.
Рассмотрим 2 метода интегрирования ДУ– метод Бернулли и метод Лагранжа.
Метод И.Бернулли
Решение уравнения y’+p(x)  y=g(x) ищется в виде произведения двух других функций, т.е. с помощью подстановки y=uv, где u=u(x) и v=v(x) - неизвестные функции от x, причем одна из них произвольна (но не равна 0 - действительно любую функцию y(x) можно записать как
y=g(x) ищется в виде произведения двух других функций, т.е. с помощью подстановки y=uv, где u=u(x) и v=v(x) - неизвестные функции от x, причем одна из них произвольна (но не равна 0 - действительно любую функцию y(x) можно записать как
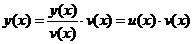 , где
, где 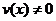 ). Тогда y’=u’
). Тогда y’=u’  v+u
v+u  v’. Подставляя выражения y и y’ в уравнение y’+p(x)
v’. Подставляя выражения y и y’ в уравнение y’+p(x)  y=g(x), получаем: u’
y=g(x), получаем: u’  v+u
v+u  v’+p(x)
v’+p(x)  u
u  v=g(x) или
v=g(x) или
u’  v+u
v+u  (v’+p(x)
(v’+p(x)  v)=g(x).
v)=g(x).
Подберем функцию v=v(x) так, чтобы выражение в скобках было равно 0, т.е. решим ДУ v’+p(x)  v=0.
v=0.
Итак, 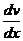 + p(x)
+ p(x)  v=0, т.е.
v=0, т.е. 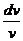 =-p(x)
=-p(x)  dx.
dx.
Интегрируя, получаем:
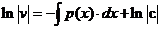
Ввиду свободы выбора функции v(x), можно принять с=1.
Отсюда 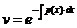
Подставляя найденную функцию v в уравнение u’  v+u
v+u  (v’+p(x)
(v’+p(x)  v)=g(x), получаем
v)=g(x), получаем
u’ 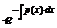 =g(x).
=g(x).
Получено уравнение с разделяющимися переменными. Решаем его:
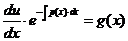 ,
, 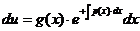 ,
,
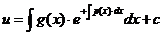
Возвращаясь к переменной y, получаем решение
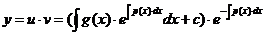 исходного ДУ y’+p(x)
исходного ДУ y’+p(x)  y=g(x).
y=g(x).
 2018-02-14
2018-02-14 750
750








