Схема двухфакторного анализа

Исследуемая переменная у определяется теперь двумя факторами A и В с p и q уровнями соответственно. На каждой из pq комбинаций уровней доступно по одному наблюдению. Для N=pq выборок единичного объема постулируется модель ,

где m, a_i, b_j – параметры, u_ij – случайная компонента с теми же свойствами, что и в однофакторном ДА. Условий репараметризации здесь два: .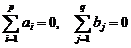

Применяя МНК, находят оценки параметров: , ,

Основная задача двухфакторного ДА – проверка равенства нулю параметров a_i и b_j, т.е. проверка гипотез: Н_А: а ₁=а₂=…= а_р =0 и Н_В: b ₁= b ₂=…= b_q= 0.

Как и в однофакторном ДА, общую сумму квадратов S ₀ отклонений от общего среднего можно разложить на составляющие – теперь уже три: S_A = , S _B = , обусловленные изменчивостью между уровнями факторов А и В соответственно, плюс слагаемое , связанное со случайной составляющей (экспериментальная ошибка).

Схема вывода соотношения S ₀ =S_A+S_B+S_R (5.5) та же, что и в однофакторном ДА.

За основу положено тождество: .

Исходные данные и результаты двухфакторного ДА принято представлять в виде табл.13 и 14.

Таблица13

Уровни фактора А	Уровни фактора В	Среднее по строкам
Уровни фактора А	1 2 … q	Среднее по строкам
1 2 p	… … …
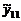Среднее по столбцам	…

Таблица 14

Источник изменчивости	Сумма квадратов	ЧСС	Среднее квадратов	F -отношение
Фактор А	S_A	p -1
Фактор В	S_B	q -1
Ошибка	S_R	(p -1)´(q -1)
	S ₀	pq -1

Гипотеза Н_А (Н_В) считается приемлемой, если F_A £ F _Т _А (F_В £ F _Т _В), где F _Т _А, F _Т _В – табличные значения F -распределения с ЧСС числителя и знаменателя в соответствии с табл.14.

Концепция «простой структуры в факторном анализе.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4

Экспериментальные критерии планирования эксперимента.

Экспериментальные критерии планирования эксперимента.

Все многообразие критериев планирования эксперимента можно разбить на две большие группы

Вторую группу составляют критерии, зародившиеся в практике планирования эксперимента и ориентированные на удобство расчетов и организации проведения экспериментов (критерии ортогональности и композиционности).

Смысл перечисленных критериев можно пояснить, используя понятие эллипсоида рассеяния случайного вектора. Для случайного вектора а размерности , ковариационная матрица которого есть cov a, эллипсоид рассеяния задается выражением ,

описывающим эллипсоид в -мерном пространстве с центром в точке Ма. Эта геометрическая фигура имеет такие размеры, что ковариационная матрица случайного вектора, равномерно распределенного в пределах эллипсоида, совпадает с матрицей cov a. Следовательно, чем больше рассеяние вектора относительно его математического ожидания, тем большие размеры имеет эллипсоид рассеяния.

Критерий ортогональности Критерий ортогональности требует выбора плана , обеспечивающего диагональность информационной матрицы. Использование этого критерия имеет целью упростить вычисления и обеспечить независимость оценок коэффициентов регрессии.

Критерий композиционности Критерий композиционности требует выбора плана, который включал бы в себя точки оптимального плана моделей более низкого порядка. Это обеспечивает сокращение числа опытов при поэтапном усложнении модели.

На практике желательно использовать планы, удовлетворяющие одновременно нескольким критериям. В общем случае такого сочетания свойств не наблюдается. В теории планирования эксперимента доказано, что непрерывный D -оптимальный план является также G -оптимальным. Условие D -оптимальности дискретного плана имеет следующий вид: . (6.2)

Если для дискретного D -оптимального плана имеет место , то этот план является также A -оптимальным.

Построение D -оптимальных планов является сложной вычислительной задачей. Аналитический путь здесь оказывается возможным в некоторых простейших случаях (полиномиальная модель от одной переменной, квадратичная регрессия от переменных для стандартной области (гиперкуб)). В общем случае для построения D -оптимальных планов используются численные методы, связанные с минимизацией определителя матрицы С либо максимизацией определителя информационной матрицы F’F, что несомненно проще в вычислительном отношении.

Выделение факторов в факторном анализе.

Выделение факторов. Выделение факторов предполагает установление числа и направления осей координат, соответствующих общим факторам, необходимым для отображения корреляции исходных переменных. С алгебраической точки зрения проблема факторов означает определение ранга матрицы А и оценивание ее элементов. Для решения задачи выделения факторов разработано достаточно много методов, однако основными в настоящее время следует признать два: метод главных факторов, наиболее широко употребляемый на практике, и метод максимального правдоподобия, имеющий прочный математико-статистический фундамент.

Метод главных факторов. Как следует из фундаментальной теоремы факторного анализа (11.3), 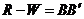. Приравняем вначале W нулевой матрице. Получим матричное уравнение 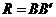. (11.6)

Матричное уравнение (11.6) имеет множество решений: любое ортогональное преобразование Т, переводящее матрицу В в G, т.е. G = ВТ, удовлетворяет (11.6). Действительно, в силу ортогональности Т имеет место 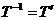и, значит, 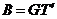. Подставляя выражение для В в (11.6), получаем 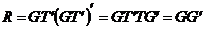, поскольку T′T=I.

Как известно из линейной алгебры, ортогональное преобразование системы координат означает поворот системы как целого на некоторый угол вокруг начала координат. Выделяя некоторое предпочтительное направление и фиксируя тем самым угол поворота системы координат, можно обойти проблему неоднозначности решения системы (11.6).

Вернемся на время к методу главных компонент. Выбор осей координат здесь подчинен определенному требованию: каждая следующая ось ориентирована по направлению максимальной дисперсии в пространстве, ортогональном предыдущим главным компонентам. Матрица весовых коэффициентов А при этом составлена из собственных векторов ковариационной (корреляционной R) матрицы. Следовательно,

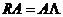, (11.7)

где 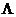– диагональная матрицa с элементами, равными собственным значениям корреляционной матрицы. Умножая (11.7) на 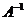справа и учитывая ортогональность A, а значит 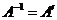, получаем: .

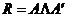Обозначим через 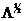матрицу порядка 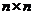, элементы которой равняются квадратному корню из соответствующих элементов матрицы Λ. Перейдем от A к 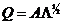. Выражение для R примет вид:

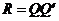. (11.8)

Сравнивая (11.6) и (11.8), получаем, что в качестве оценки матрицы В можно взять матрицу .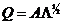

Таким образом, матрица факторных нагрузок получается из матрицы, составленной из собственных векторов корреляционной матрицы исходных признаков, с последующим умножением элементов собственного вектора, отвечающего i -му собственному значению 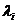на .

Матрицы B и Q имеют разный порядок: 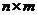у В и 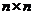у Q, поэтому правильнее говорить, что оценкой будут первые m столбцов матрицы Q.

Посчитав матрицу W равной нулю, мы для оценки матрицы B воспользовались моделью главных компонент. Строго говоря, под методом главных факторов понимают способ расчета, принятый в методе главных компонент, но примененный к матрице 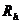(оценка общностей рассматривается ниже).

0ценка числа общих факторов. Общепризнанного метода определения числа m общих факторов, подлежащих выделению, не существует. Однако разработан ряд критериев, с помощью которых можно сделать достаточно обоснованное заключение.

Широкое применение получил сравнительно простой критерий собственных значений: выделять только те факторы, которые соответствуют собственным значениям, большим единицы.

Рассмотрим матрицу 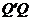.Справедлива следующая цепочка равенств: .

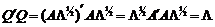Полученное соотношение показывает, что сумма квадратов нагрузок i -го общего фактора на исходные признаки равняется i -му собственному значению 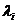. Но 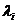характеризует вклад i -го общего фактора в полную дисперсию (напомним, что полная дисперсия равняется следу корреляционной матрицы R и 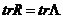). Поэтому факторы, вклады которых меньше единицы, имеют долю дисперсии, меньшую единичной дисперсии исходных признаков, и их нецелесообразно включать в число общих факторов.

Считается также, что вклад общих факторов в суммарную общность должен составлять около 90%, а число общих факторов не должно превышать половины числа исходных признаков, т.е. m<n/ 2, а более точно, .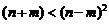

К проблеме оценки числа факторов можно подойти со статистической точки зрения. Ранее отмечалось, что если коэффициенты корреляции после учета m факторов незначимо отличаются от нуля, то нет необходимости вводить (m+ 1) - й фактор. Другими словами, равенство 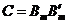должно выполняться в статистическом смысле (здесь 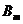− матрица факторных нагрузок с числом факторов, равным m). Для оценки значимости матрицы R (в самом начале факторного анализа) либо матрицы 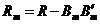используется критерий Бартлетта − Уилкса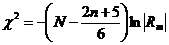

с n (n- 1) / 2 степенями свободы, либо его аппроксимация 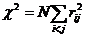, где 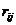– элементы матрицы .

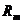Если все эти критерии дают не противоречащие друг другу решения, то удовлетворяются этими m факторами.

Метод максимального правдоподобия. В этом методе по выборочной корреляционной матрице 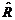исходных признаков ищутся состоятельные и эффективные оценки неизвестных параметров − элементов матриц В и W для генеральной совокупности. При построении функции максимального правдоподобия существенно используются предпосылки факторного анализа. Максимизация функции правдоподобия приводит к множественности результатов. Неоднозначность обходится требованием, чтобы матрица

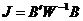(11.9)

имела диагональный вид. Это условие соответствует требованию метода главных факторов о взаимной ортогональности факторов и их ориентации по направлению максимума дисперсии.

Система (11.9) может быть приведена к виду, удобному для вычислений итерационным путем:

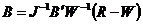. (11.10)

Скорость сходимости итерационной процедуры является весьма медленной и зависит от начального приближения B и W.

В методе максимального правдоподобия проблема определения числа факторов также существует. Пусть расчеты по (11.10) проведены для m общих факторов. Для проверки гипотезы о существовании m общих факторов можно воспользоваться критерием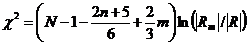

c 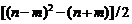степенями свободы.

В этой формуле 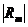– определитель матрицы корреляций, воспроизведенных с помощью m общих факторов. Если вычисленное значение критерия превышает табличное значение 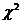при выбранном уровне значимости, то необходимо выделить факторов больше, чем m, по крайней мере, m+ 1.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5

Теоретические критерии планирования эксперимента.

Теоретические критерии планирования эксперимента.

Все многообразие критериев планирования эксперимента можно разбить на две большие группы. Первую составляют критерии, непосредственно учитывающие точностные свойства получаемых оценок. Среди них можно выделить критерии, связанные с точностью нахождения коэффициентов регрессии (критерии A - и D -оптимальности), и критерии, требующие максимальной точности оценки выходной переменной (критерий G -оптимальности).

Критерий А-оптимальности Поскольку точностной характеристикой вектора коэффициентов регрессии является ковариационная матрица, а критерии планирования желательно иметь в скалярной форме, то необходима некоторая свертка ковариационной матрицы. Критерий A-оптимальности в качестве такой свертки использует след матрицы . Поскольку диагональные элементы матрицы С пропорциональны дисперсии оценок коэффициентов регрессии, то при минимизации следа матрицы С минимизируется, по сути дела, суммарная либо средняя дисперсия оценок коэффициентов модели: .

Известно, что сумма диагональных элементов матрицы равняется сумме её собственных значений. Поскольку квадраты длины осей эллипсоида рассеяния пропорциональны собственным значениям ковариационной матрицы, то критерий A-оптимальности требует минимизации диагонали параллелепипеда, описанного у эллипсоида рассеяния.

Критерий D-оптимальности Критерий D -оптимальности требует такого расположения точек в области планирования 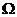, при котором определитель матрицы имеет минимальную величину. Иными словами, план D -оптимален, если .

Известно, что объем эллипсоида рассеяния пропорционален корню из величины определителя ковариационной матрицы, т.е. . С учетом (3.8) V ~ .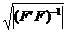

Чем меньше величина определителя, тем меньше, как правило, разброс оценок коэффициентов относительно их математических ожиданий. Исключением является случай, когда эллипсоид рассеяния имеет сильно вытянутую форму.

Критерий G-оптимальности План G-оптимален, если он обеспечивает наименьшую величину максимальной дисперсии оценки зависимой переменной: .