2018-02-14
867
Если при движении в потоке частицы жидкости не вращаются, то такое движение является потенциальным.
Условия потенциального течения имеют вид:
1. 
, где 
– характеризует интенсивность вихревого поля в каждой его точке.
2. Угловые скорости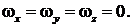 
3. Для потенциального течения имеем:
Три последних условия являются необходимыми и достаточными, чтобы существовала функция 
, называемая потенциальной, полный дифференциал которой равен: 
.
Представляя полный дифференциал функции как
,
получаем 
Доказано, что распределение поля скоростей описывается уравнением Лапласа:
.
Для плоских течений, если выполняется условие
,
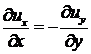то существует функция 
– функция тока, для которой выполняется 
Учитывая, что полный дифференциал 
, следовательно,
.
Течение будет вихревым, если частицы в потоке жидкости вращаются, т.е.
.
Совокупность векторов угловых скоростей в различных точках потока образуют векторное поле – поле угловых скоростей. Это векторное поле может быть как стационарным, так и нестационарным. Вихревое течение характеризуется вихревыми линиями. Линия, касательная к которой в каждой точке в данный момент времени определяет направление вектора угловой скорости 
, называется вихревой линией. Совокупность вихревых линий, пронизывающих элементарный контур 
, образует вихревую трубку или вихревую нить.
Вихревые трубки (нити) характеризуются интенсивностью (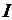
), для которой справедливо
.
Чтобы рассчитать интенсивность вихревого течения пользуются теоремой Стокса: циркуляция вектора 
по замкнутому контуру 
равна интенсивности вихревого течения
.
При этом интенсивность вихревого течения не зависит от размеров и формы контура, а зависит от размера вихревой зоны.
Установившееся и неустановившееся
Течения жидкости
При неустановившемся течении скорость и давление в каждой точке пространства изменяется с течением времени, т. е. 
.
При установившемся (стационарном) течении скорость в каждой точке пространства в различные моменты времени не меняет своей величины и направления, поэтому 
. Поэтому в случае установившегося течения
.
При установившемся течении траектории движения частиц, проходящие через одну и ту же точку пространства, совпадают друг с другом и не меняют своей формы с течением времени.
Установившееся движение может быть равномерным и неравномерным.
Равномерным движением называется такое движение, при котором скорости в сходственных точках двух смежных сечений равны между собой, а траектории частиц – прямолинейны и параллельны оси ох, т.е. поле скоростей не изменяется вниз по течению. Ускорение частиц жидкости при этом равно нулю.
Неравномерное движение – это движение, не удовлетворяющее определению равномерного движения.
Равномерное и неравномерное движение может быть напорным и безнапорным. При напорном движении жидкость соприкасается с твердой стенкой по всему периметру своего сечения, а при безнапор-
ном – лишь по части периметра.
Таким образом:
1. Когда скорость в отдельных точках пространства изменяется относительно медленно, поэтому величинами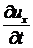 
, 
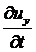, можно пренебречь.
2. Когда скорость в отдельных точках пространства изменяется относительно быстро, тогда эти ускорения учитывать необходимо.
