Изображение гармонических колебаний

Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями (рис.4 и 5)

Рис.4. Колебания груза на пружине. Трения нет.

Рис.5 Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = lφ – смещение маятника по дуге.

Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам:

· Колебания встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;

· Различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний.

Рассмотрим сначала уравнение свободных колебаний

(1)

Напишем соответствующее характеристическое уравнение

и найдем его корни:

1) Пусть Тогда корни – действительные отрицательные числа. Общее решение выражается через показательные функции:

(2)

Из этой формулы следует, что отклонение при любых начальных условиях асимптотически стремится к нулю, если В данном случае колебаний не будет, так как силы сопротивления велики по сравнению с коэффициентом жесткости рессоры

2) Пусть тогда корни равны между собой (и равны отрицательному числу ). Поэтому общее решение будет

(3)

Здесь отклонение также стремится к нулю при , однако не так быстро, как в предыдущем случае (благодаря наличию сомножителя ).

3) Пусть то есть отсутствует сила сопротивления. Уравнение (1) примет вид

(4)

аракткристическое уравнение имеет вид а его корни равны Общее решение

(5)

В последней формуле произвольные постоянные заменим другими. Именно, введем постоянные связанные с соотношениями

, .

через определяются так:

, .

Подставляя значения в формулу (5), будем иметь

Или

(6)

Колебания в этом случае называются гармоническими. Интегральными кривыми являются синусоиды. Промежуток времени , за который аргумент синуса изменяется на , называется периодом колебаний; в данном случае Частотой колебания называется число колебаний за время ; в данном случае частота равна 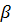; - величина наибольшего отклонения от положения равновесия – называется амплитудой колебания; называется начальной фазой. График функции (6) изображен на рис.6