Запись гармонических колебаний в комплексной форме

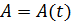Рассмотрим в комплексной плоскости  радиус- вектор  постоянной длины  Конец вектора  при изменении параметра t (в данном случае t - время) описывает окружность радиуса  с центром в начале координат (рис.7)

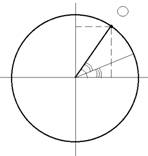
Рис.7

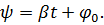Пусть угол ψ, образованный вектором  и осью , выражается так:  Величина  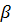называется угловой скоростью вращения вектора . Проекции вектора  на оси  и

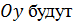
, . (7)

Выражения (7) суть решения уравнения (4).

Рассмотрим комплексную величину

Или

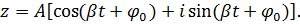  (8)

В декартовой системе координат действительную часть комплексного числа обычно откладывают по оси абсцисс, а мнимую - по оси ординат (см. рис.7). Следовательно, любое комплексное число можно представить в виде вектора A на комплексной плоскости, проведенного из начала координат в точку с координатами {x; y}.

Таким образом, решения уравнения гармонических колебаний (4) можно рассматривать как проекции вектора  на оси  и , вращающегося с угловой скоростью 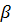 при начальной фазе

 Пользуясь формулой Эйлера

e^iα = cos α +i·sin α,

где i = (-1)^1/2 - мнимая единица, выражение (8) можно переписать так:

 (9)

Мнимая и действительная части выражения (9) являются решениями уравнения (4). Выражение (9) называется комплексным решением уравнения (4). Перепишем выражение (9) так:

. (10)

Выражение называют комплексной амплитудой. Обозначим ее через 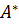. Тогда комплексное решение (10) перепишется так:

. (11)

4) Пусть . В этом случае корни характеристического уравнения – комплексные числа

где

Общий интеграл имеет вид

 (12)

Или

 (13)

Здесь в качестве амплитуды приходится рассматривать величину , зависящую от времени. Так как , то она стремится к нулю при , то есть здесь мы имеем дело с затухающими колебаниями. График затухающих колебаний изображен на рис.8.

Рис.8