2014-02-09
1352
Рисунок 8.5
Рисунок 8.4
Найдем выражение для комплексной амплитуды тока, пользуясь соотношением: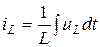 
.
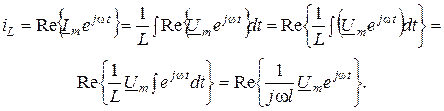
Сократив выражение на множитель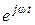 
, получаем еще одну запись закона Ома в комплексной форме:
,
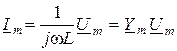где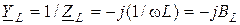 
- комплексная проводимость индуктивности.
Укажем, что операция интегрирования реальной функции времени при переходе к комплексно-временной функции заменяется операцией деления на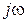 
.
8.3 Синусоидный ток в емкости
Пусть через емкость протекает ток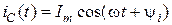 
. Мгновенные значения тока и напряжения в емкости связаны соотношениеми:
; 
.
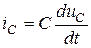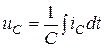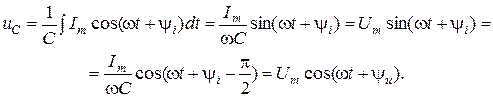
Анализ последнего выражения показывает:
1) 
; 
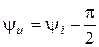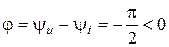, ведь напряжение в емкости отстает от тока по фазе на угол 
;
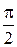2) амплитуды, равно как и реальные значения напряжения и тока, связаны законом Ома: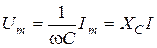 
; 
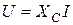. Величина 
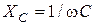, которая имеет размерность Ом, носит название емкостного сопротивления; обратная к ней величина 
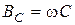носит название емкостной проводимости. Тогда 
; 
.
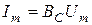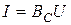Мгновенная мощность энергии, которая поступает в емкости, представляет:
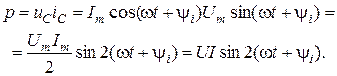
Активная мощность P = 0, равно как и для индуктивности. Энергия электрического поля в емкости определяется по формуле:
;
.
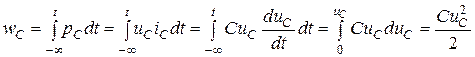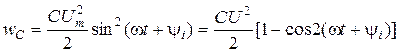Зависимость мгновенных значений u, i, p,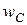 
в емкости по времени изображена на рис.8.5. Равно как и в индуктивности, происходит колебание энергии между источником и емкостью, причем активная мощность равняется нулю.
Если перейти к комплексно-временным функциям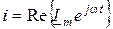 
; 
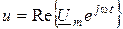и подать с их помощью мгновенные значения, можно найти выражения для комплексных амплитуд тока и напряжения:
; 
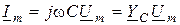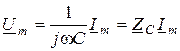, (8.3)
где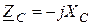 
; 
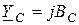- комплексные сопротивление и проводимость емкости.
Полученное выражение - это закон Ома в комплексной форме для емкости. Чтобы рассмотреть фазовые соотношения, запишем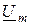 
и множитель -j в показательной форме:
.
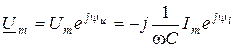
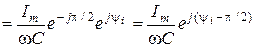Это выражение подтверждает вывод, что в емкости напряжение отстает по фазе от тока на угол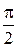 
(рис.8.4б).
Рассмотрим применение метода комплексных амплитуд для электрических цепей с последовательным и параллельным соединением элементов R, L и C.
9.1 Последовательное соединение элементов R, L, C
Рассмотрим электрическую цепь, которая состоит из последовательно соединенных элементов R, L, C. Запишем согласно со вторым законом Кирхгофа уравнения для мгновенных значений падений напряжени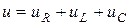й: 
, или
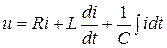. (9.1)
Если перейти к комплексно-временным функциям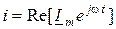 
, 
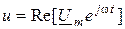и подставить их значения к уравнения (9.1), найдем выражение для комплексных амплитуд:
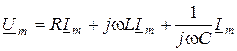. (9.2)
С учетом выражений (8.1)-(8.3) получаем второй закон Кирхгофа в комплексной форме:
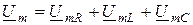. (9.3)
Если вынести за скобки значения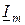 
, будем иметь
,
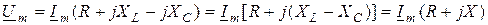где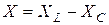 
- реактивное сопротивление цепи; R - активное сопротивление;
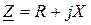- комплексное сопротивление цепи.
С учетом введенных определений будем иметь уравнения
, 
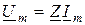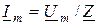, (9.4)
которые подают закон Ома в комплексной форме.
Комплексное сопротивление можно подать в тригонометричной и показательной формах:
, 
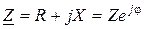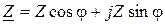, (9.5)
где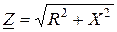 
- модуль комплексного сопротивления 
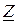(полное электрическое сопротивление цепи); 
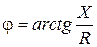- аргумент комплексного сопротивления; 
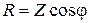- активное сопротивление, которое равняется реальной части ; 
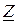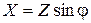- реактивное сопротивление, которое равняется мнимой части .
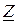Согласно с (9.4) комплексное сопротивление цепи 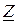- это комплексная величина, которая равняется части от деления комплексной амплитуды напряжения на зажимах двуполюсника на комплексный ток.:
,
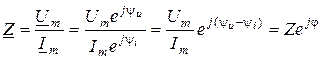где Z - полное сопротивление;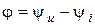 
- аргумент комплексного сопротивления.
Итак, полное сопротивление цепи (модуль 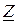) устанавливает связь между амплитудами (действующими значениями) тока и напряжения, а аргумент комплексного сопротивления совпадает со сдвигом фаз между напряжением и током.
Рассмотрим геометрическую интерпретацию закона Ома и второго закона Кирхгофа в комплексной форме с помощью векторной диаграммы.
Векторная диаграмма - изображение векторов на комплексной плоскости для одного и того же момента времени с соблюдением фазовых соотношений. Момент времени может быть любой, поскольку взаимная ориентация векторов не изменяется.
Рассмотрим векторные диаграммы для двух случаев.
1) 
, 
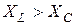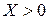. Обозначим в уравнении (9.3) 
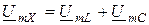- напряжение на реактивном участке цепи. Напряжение на активном ребре 
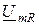совпадает по фазе с током 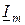, напряжение на индуктивности 
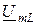опережает ток на угол 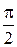, а напряжение на емкости 
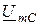отстает от тока на угол 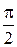(рис.9.1а). Итак, общее напряжение 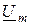опережает ток 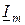по фазе на угол 
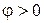. Положительный фазовый сдвиг соответствует индуктивному характеру сопротивления цепи .
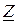2) 
, 
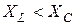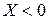(рис.9.1,б). В этом случае реактивное сопротивление цепи имеет емкостной характер (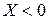), ведь общее напряжение отстает по фазе от тока на угол 
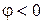. Отрицательный фазовый сдвиг соответствует емкостному характеру сопротивления .
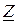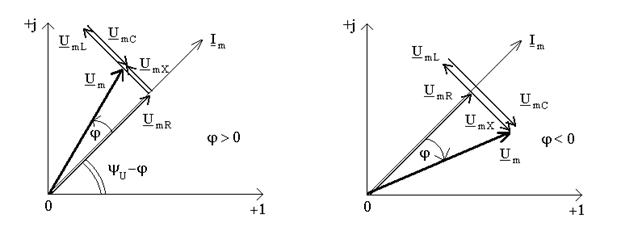
а) б)
