Алгебра комплексных чисел

Комплексным числом называют пару чисел, изображающих вектор на комплексной плоскости. Будем изображать комплексное число заглавной буквой с чертой внизу (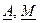). Вводится мнимая единица:

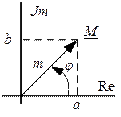
Комплексное число может быть представлено в разных формах:

– показательная форма: - это вектор на комплексной плоскости, где- длина (модуль) вектора, - аргумент или фаза. Фазу всегда отсчитывают против часовой стрелки от положительного направления вещественной оси;

– алгебраическая форма: 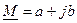– это точка на комплексной плоскости, где - координаты по вещественной и мнимой осям, причем:

, ,

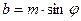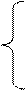
, если ,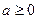

=

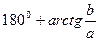, если <.

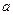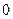Переход от одной формы записи комплексного числа к другой:

.

Складывать комплексные числа предпочтительно в алгебраической форме либо геометрически по правилу параллелограмма: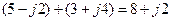

Вычитать комплексные числа удобно в алгебраической форме либо геометрически по правилу параллелограмма (вектор разности направлен из конца вычитаемого в конец уменьшаемого):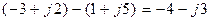

Умножать и делить комплексные числа удобнее в показательной форме:

; .

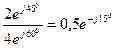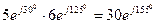Комплексные числа, не зависящие от времени, обозначают заглавными буквами с чертой внизу: , а комплексно сопряженные им числа обозначают еще и звездочкой сверху: это числа, у которых та же вещественная часть, а мнимая с обратным знаком.

Комплексные числа, которые являются функциями времени, обозначают заглавными буквами с точкой сверху: 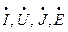, а комплексно сопряженные им числа обозначают заглавными буквами со звездочкой сверху 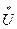: это числа, у которых тот же модуль, но фаза с обратным знаком.

Так как , то умножить комплексное число на j это значит, не изменяя его модуля, увеличить фазу на 90⁰ или повернуть соответствующий вектор на 90⁰ против часовой стрелки. Разделить на j - наоборот:

.