2018-02-14
309
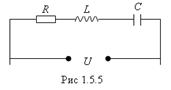
Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний включают последовательно с элементами контура переменную ЭДС или подают на контур переменное напряжение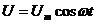 
(рис.1.5.5). Цепь, в которой последовательно с ЭДС включены сопротивление R, индуктивность L и конденсатор С, называется последовательным колебательным контуром.
По второму правилу Кирхгофа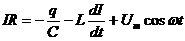 
или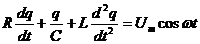 
, разделив на L: 
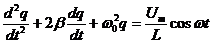(29) - уравнение вынужденных колебаний
Частное решение (29):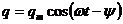 
(30), 
или подставляя 
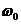и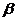 
: 
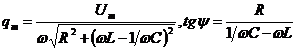- амплитуда заряда на конденсаторе и разность фаз между приложенным напряжением и зарядом.
Общее решение получится, если к частному решению (30) прибавить общее решение однородного дифференциального уравнения, которое было получено в предыдущем параграфе. Оно содержит множитель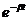 
, который очень быстро убывает, и при прошествии достаточно большого времени 
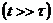им можно пренебречь. Установившиеся вынужденные электромагнитные колебания в контуре описываются уравнением (30).
Силу тока в контуре при установившихся колебаниях найдем, продифференцировав (30) по времени: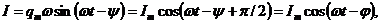 
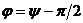- сдвиг фаз между током и приложенным напряжением 
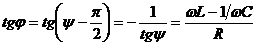- ток отстает по фазе от напряжения (
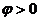)при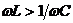 
и опережает напряжение (
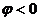) при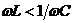 
. Амплитуда силы тока 
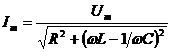(31).
Представим соотношение (29) в виде: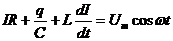 
, 
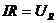- падение напряжения на активном сопротивлении; 
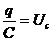- падение напряжения на конденсаторе; 
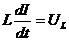– напряжение на индуктивности.
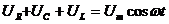(32) - сумма напряжений на отдельных участках контура равна в каждый момент времени напряжению, приложенному извне.
Сравнивая напряжение на элементах цепи и ток в цепи:
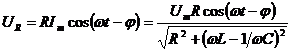- напряжение на активном сопротивлении совпадает по фазе с током в контуре; н апряжение на конденсаторе 
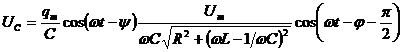отстаёт от силы тока на π /2; напряжение на индуктивности 
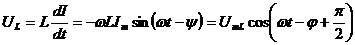напряжение на индуктивности опережает ток на π /2, 
.
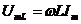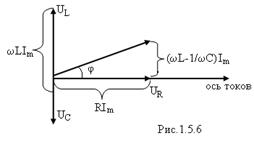Фазовые соотношения можно представить наглядно с помощью векторной диаграммы: гармонические колебания задают с помощью вектора, длина которого равна амплитуде колебаний, а направление вектора образует с некоторой осью угол, равный начальной фазе колебаний. Возьмём в качестве прямой, от которой отсчитывается начальная фаза, ось токов (рис. 1.5.6).
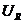совпадает по фазе с током, 
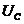– отстаёт на π /2, 
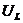опережает на π /2. Векторы 
, 
, 
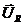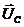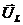в сумме дают 
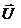, определяемое выражением (32).
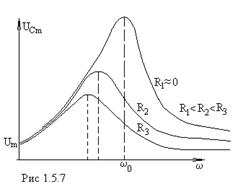При определенной частоте внешнего воздействия в контуре наступает резонанс. Резонансная частота для напряжения на конденсаторе 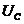и для заряда q:
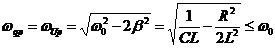. Резонансные кривые для напряжения на конденсаторе 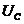представлены на рис.1.5.7. Все резонансные частоты меньше собственной частоты колебаний 
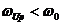. При ω→0 резонансные кривые сходятся в одной точке 
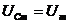– напряжение на конденсаторе при подключении его к источнику постоянного напряжения 
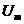. Максимум при резонансе тем острее и выше, чем меньше затухание β=R /2 L, чем меньше R и больше L. Ход резонансной кривой аналогичен резонансной кривой при механических колебаниях.
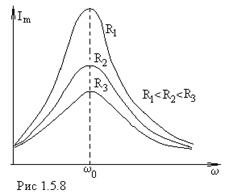Резонансные кривые для тока приведены на рис.1.5.8. Амплитуда силы тока максимальна, когда 
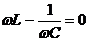- резонансная частота для силы тока совпадает с собственной частотой колебаний: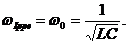 
При ω →0 сила тока уменьшается до нуля, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.
При малом затухании (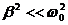
) резонансную частоту для напряжения можно считать равной 
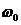. Добротность контура 
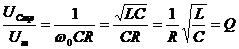- отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешнего напряжения и показывает, во сколько раз напряжение на конденсаторе может превышать приложенное напряжение.
При резонансе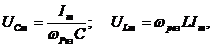 
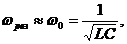
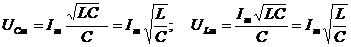- амплитуды напряжений на ёмкости и индуктивности равны между собой, но противоположны по фазе. Напряжения на ёмкости и индуктивности компенсируют друг друга, и цепь ведёт себя как цепь только с активным сопротивлением. Вся энергия, приложенная к контуру, идёт на Ленц-Джоулево тепло. Ток в цепи достигает максимального значения - резонанс напряжений – и ндуктивного 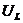и емкостного .
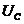РЕЗОНАНС В ПАРАЛЛЕЛЬНОМ КОНТУРЕ
Рассмотрим колебательный контур, в котором индуктивность L и ёмкость С соединены параллельно (рис.1.5.9). Активное сопротивление близким к нулю, R ≈0. Амплитуда напряжений на индуктивности и ёмкости: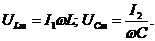 
По второму правилу Кирхгофа 
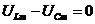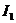токи 
и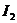 
в каждый момент времени находятся в противофазе: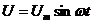 
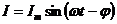
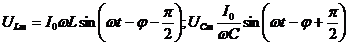. Ток в неразветвленной цепи равен 
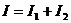, или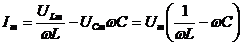 
.
При 1 /ωL=ωC ток I =0 - условие резонанса токов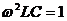 
– частота колебаний равна собственной: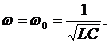 
ПЕРЕМЕННЫЙ ТОК
Установившиеся вынужденные колебания можно рассматривать как протекание в цепи, обладающей ёмкостью, индуктивностью и активным сопротивлением, переменного тока, который обусловлен переменным напряжением: 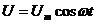. Ток изменяется по закону 
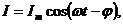амплитуда тока 
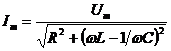. Ток отстаёт от напряжения по фазе на угол 
: 
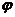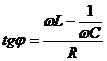. Если 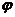<0, ток опережает напряжение.
Полное электрическое сопротивление (импеданс)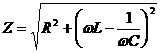 
, R - активное сопротивление, 
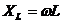- реактивное индуктивное сопротивление, 
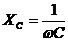- реактивное емкостное сопротивление. Ток на индуктивности отстаёт от напряжения на π /2, а ток на емкости опережает напряжение на π /2.
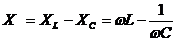- реактивное сопротивление (реактанс). 
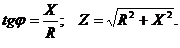Если значения сопротивлений R и X отложить вдоль катетов треугольника, то длина гипотенузы будет численно равна Z (рис.1.5.10). Мощность, выделяемая в цепи переменного тока: 
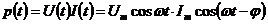, используя тригонометрию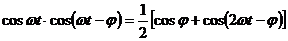 
.
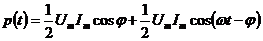Среднее значение мощности (учитывая, что среднее значение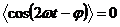 
) 
, 
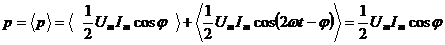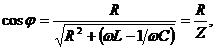
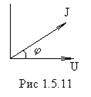
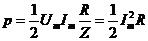(рис.1.5.11) - такую же мощность развивает постоянный ток силой 
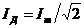- эффективная сила тока (действующая).
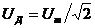- действующее напряжения.
Средняя мощность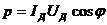 
; 
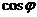- коэффициент мощности. Чем меньше 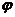, тем ближе 
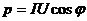к 1, тем больше мощность.
