2018-02-14
217
Современная теоретическая физика располагает различными приемами, направленными, как минимум, на анализ фундаментальных уравнений. Известны определенные классы функций, удовлетворяющих упрощенному волновому уравнению. Одними из наиболее характерных решений являются классы плоских и сферических волн.
Плоская волна:
,
где 
– радиус вектор в направлении возрастания значений,
– единичный вектор нормали к поверхности волны,
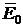– вектор амплитуды электрического поля.
Соотношение для плоской волны несложно подставить в волновое уравнение, в результате чего будет получено тождество.
Сферическая волна:
.
Эта формулировка аналогично удовлетворяет волновому уравнению.
Очень часто вместо функции поля используют ее комплексный аналог, позволяющий избавиться в явном виде от гармонических функций (перевести их в экспоненциальную форму, но в комплексном представлении)
,
,
где 
– волновой вектор,
– полная фаза световой волны (в радианах).
Для случая 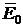=const, используя уравнения Максвелла, несложно установить связь между напряженностями магнитного и электрического полей
|
|
|
,
из чего однозначно следует, что вектора 
конфигурируются, как правая тройка векторов.
Несложно установить, что энергия электромагнитной волны делится на две равных составляющие: магнитную и электрическую
,
но при этом за счет того, что диэлектрическая составляющая может существенно отличаться от единицы, то для баланса энергий напряженность электрического поля должна быть в 
раз меньше напряженности магнитного поля.
