Проведение измерений и обработка результатов

ЛАБОРАТОРНАЯ РАБОТА № 6

 

ИЗУЧЕНИЕ ЯВЛЕНИЯ ПОЛЯРИЗАЦИИ СВЕТА

(ЗАКОН МАЛЮСА)

 

Цель работы: изучение зависимости освещённости экрана фотоэлемента от угла поворота оптической оси одного поляроида относительно другого.

 

Приборы: источник света, фотоэлемент, люксметр, два поляроида.

 

Теоретические сведения

 

С точки зрения электродинамики свет представляет собой поперечные электромагнитные волны. Векторы напряжённости электрического поля  (световой вектор) и магнитного поля  колеблются во взаимно перпендикулярных плоскостях. Вектор Умова – Пойтинга  характеризует направление распространения волны, то есть направление распространения энергии электромагнитных колебаний (рис. 16).

Рис. 16

При взаимодействии света с веществом переменное электрическое поле воздействует на отрицательно заряженные электроны атомов или молекул этого вещества, в то время как действие со стороны магнитного поля на заряженные частицы незначительно. Поэтому в процессах распространения света главную роль играет вектор электрической напряжённости.

На рис. 17 схематично показаны колебания вектора  для плоскополяризованной (а) и естественной (б) световой волны, распространяющейся перпендикулярно плоскости рисунка.

 

 

Рис. 17

В настоящей работе для получения и исследования линейнополяризованного света применяются поляроиды. Они изготовляются из очень мелких кристаллов турмалина или герапатина, нанесённых на целлулоидную плёнку. Оптические оси всех кристаллов ориентированы в одном направлении. Этим кристаллам присуще явление дихроизма, т.е. в них обыкновенный луч практически полностью поглощается на толщине . Поэтому естественный свет, проходя сквозь поляроид, становится плоскополяризованным.

 

Описание прибора

 

Рассмотрим установку, состоящую из источника света S, двух поляроидов P и A, фотоэлемента F и люксметра L (рис. 18). Пройдя сквозь первый поляроид (поляризатор) P, свет становится плоскополяризованным. Второй поляроид (анализатор) А может пропускать только те колебания, которые совпадают с его главной оптической осью АА.

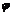Пусть  – амплитуда вектора напряжённости колебания, пропускаемого поляризатором,  – угол между главными оптическими осями поляризатора и анализатора. Амплитуду  можно разложить на две взаимно перпендикулярные составляющие, одна из которых  совпадает с главной оптической осью анализатора, вторая  – перпендикулярна ему. Таким образом, из анализатора выйдет свет с амплитудой:

.

Так как интенсивность света пропорциональна квадрату амплитуды, то

.                                  (1)

Это соотношение носит название закона Малюса.

Рис. 18

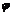Пусть  – амплитуда вектора напряжённости колебания, пропускаемого поляризатором,  – угол между главными оптическими осями поляризатора и анализатора. Амплитуду  можно разложить на две взаимно перпендикулярные составляющие, одна из которых  совпадает с главной оптической осью анализатора, вторая  – перпендикулярна ему. Таким образом, из анализатора выйдет свет с амплитудой:

.

Так как интенсивность света пропорциональна квадрату амплитуды, то

.                                  (1)

Это соотношение носит название закона Малюса.

Если свет при прохождении поляризатора полностью поляризуется, то при вращении анализатора интенсивность прошедшего через анализатор света изменяется от нуля (при ) до  (при ). Интенсивность света, прошедшего через поляризатор, равна половине интенсивности падающего на него естественного света: . Если же при прохождении света через поляризатор свет частично поляризуется, то при вращении анализатора интенсивность прошедшего света будет изменяться в пределах от  до . Тогда можно вычислить степень поляризации:

.                             (2)

 

Проведение измерений и обработка результатов

 

1. Включить источник света, вращением поляризатора Р и анализатора А установить минимальное отклонение стрелки люксметра. Это будет нулевой отсчёт прибора.

2. Вращая поляризатор или анализатор вокруг оси, снять показания люксметра через каждые 10˚ от 0˚ до 360˚.

3. Построить график в полярных координатах, откладывая по радиусу освещённость. В качестве полярного угла взять угол между главными оптическими осями поляризатора Р и анализатора А (угол ).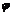

4. По полученной зависимости в полярных координатах сделать вывод о характере поляризации (эллиптическая, циркуляционная, линейная).

5. По формуле (2) рассчитать степень поляризации Р поляроидов.

 

Контрольные вопросы и задания

 

1. Рассказать об электромагнитной природе света. Что такое естественный и поляризованный свет?

2. Дать понятие оптической анизотропии. Как получить поляризованный свет при прохождении его через анизотропные кристаллы?

3. Рассказать о двойном лучепреломлении.

4. Сформулировать закон Малюса.

5. Сформулировать закон Брюстера.

6. Рассказать о поляризационных приборах и использовании поляризованных лучей.