Случайные блуждания на прямой: упрощенный случай

Рассмотрим стохастическое блуждание точки вдоль прямой «в чистом виде», т.е. вне всякой связи с динамикой. Допустим, что точка в каждый момент времени может с одинаковой вероятностью сместиться на одну единицу длины вправо или влево. Тогда имеется точный результат [2, с. 10–11]: вероятность того, что в момент времени T координата частицы будет равна k, дается следующим выражением:

. (4.6)

Для имитационного моделирования системы модифицируем программу п. 4.1. Ясно, что теперь программа будет существенно проще: не будет массива скорости, достаточно использовать только одно бинарное случайное число, расчет нового значения координаты будет выполняться по совсем простой формуле . Программа имеет вид:

> restart:

> with(stats):randomize():

> T:=10:

> MC:=100000:

> X:=vector(T):XMC:=vector(MC):

> for i from 1 to MC do XMC[i]:=0:od:

> roll_1:= rand(1..2):

> for ijk from 1 to MC do for k from 1 to T do X[k]:=0:od: for j from 1 to T-1 do q2:=roll_1(): if(q2=1) then X[j+1]:=X[j]+1:else X[j+1]:=X[j]-1:fi: od: XMC[ijk]:=X[T]:od:

> xx:= [ XMC[n] $n=1..MC]:xx2:= [ XMC[n]^2 $n=1..MC]:

> evalf(describe[mean](xx));evalf(describe[mean](xx2));

Первый результат понятен: ввиду равноправия левого и правого, среднее смещение равно нулю. Второе значение – средний квадрат смещения – явно равно 9. Вычисляя с большим количеством прогонов, т.е. увеличивая MC еще на порядок – до 10⁶, получаем еще более точное значение

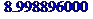Соответствует ли полученное значение среднего квадрата смещения истинному распределению вероятностей (4.6)? Вычислим вероятности по формуле (4.6), имея в виду, что в вышеприведенной программе мы фактически рассматривали не T, а T-1 шагов блужданий:

> for j from -(T-1) to T-1 do w[j]:=evalf(int(cos(phi)^(T-1)*exp(-I*phi*j),phi=-Pi..Pi)/2/Pi);od:

Любое распределение вероятностей полного (т.е. всех возможных) набора событий должно быть нормировано на единицу, что необходимо всегда обязательно проверять, вычисляя сумму всех значений вероятностей:

> sum(w[jjk],jjk=-(T-1)..T-1);

Итак, под именем w вычислено точное распределение вероятностей координат частицы после T-1 случайных шагов. Вычислим те же вероятности по результатам нашего имитационного моделирования. Для этого для каждого значения координаты, необходимо посчитать, сколько раз среди наших MC прогонов, после T-1 шагов,получалось это значение координаты, и разделить на MC:

> for y from –(T-1) to T-1 do S[y]:=0:for jj from 1 to MC do if(XMC[jj]=y) then S[y]:=S[y]+1:fi: od:P[y]:=evalf(S[y]/MC):od:

По терминологии математической статистики, P – это так называемые выборочные значения вероятностей (фактически выборочные частоты), т.е. полученные из выборки конечного объема, в данном случае MC. Сравним выборочные вероятности для объема MC=100000 и точные, распечатав их в формате list (простой список):

> [P[a] $a=0..T-1];

> [w[a] $a=0..T-1];

Видим, что имеется хорошее совпадение выборочного и точного распределений. По закону больших чисел, при увеличении объема выборки выборочные значения должны все более приближаться к истинным. Читателю предоставляется убедиться в этом, увеличив MC на порядок.

Наконец, вычислим средний квадрат координаты по точному распределению вероятностей w:

> sum(w[jjk]*jjk^2,jjk=-(T-1)..T-1);