Детерминированная задача оптимизации

Рассматривая статистическую задачу оптимизации, мы считали входной сигнал случайным процессом и минимизировали средний квадрат ошибки воспроизведения образцового сигнала. Однако возможен и иной подход, не использующий статистические методы.

Пусть, как и раньше, обработке подвергается последовательность, состоящая из К отсчетов x(k), коэффициенты нерекурсивного фильтра образуют вектор-столбец w, a отсчеты образцового сигнала равны d(k). Выходной сигнал фильтра определяется формулой (5.1), а ошибка воспроизведения образ­цового сигнала – формулой (5.2).

Теперь оп­тимизационная задача формулируется так: необходимо найти такие коэффициенты фильт­ра w, чтобы норма ошибки воспроизведения образцового сигнала была минимальной:

.                                    (5.10)

Для решения задачи в выражениях (5.1) и (5.2) перейдем к матричной запи­си, получая формулы для векторов-столбцов выходного сигнала у и для ошибки воспроизведения входного сигнала е:

y = U^Tw, e=d - U^Tw.                                      (5.11)

Здесь d – вектор-столбец отсчетов образ­цового сигнала, a U – матрица, столбцы которой представляют собой содержимое ли­нии задержки фильтра на разных тактах

U=[u(0), u(1),…, u(K-1)].

Выражение (5.10) для нормы ошибки можно переписать в матричном виде следующим об­разом:

J(w)=e 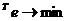.                                   (5.12)

Подставляя (5.11) в (5.12), получаем

J(w) = (d - U^Tw)^T (d - U^T w) = d^Td - w^TUd - .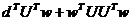

Для нахождения минимума необходимо вычислить градиент данного функционала и приравнять его нулю:

grad J(w) = -2Ud + 2UU^T w = 0.

Отсюда легко получается искомое опти­мальное решение:

w = (UU 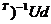.                                           (5.13)

В формуле (5.13) прослеживается близкое родство с формулой (5.5), описывающей опти­мальный в статистическом смысле фильтр Винера. Действительно, если учесть, что (UU     дает оценку корреляционной матрицы сигнала, полученную по одной реа­лизации сигнала путем временного усредне­ния, a Ud / К является аналогичной оценкой взаимных корреляций между образцовым сиг­налом и содержимым линии задержки фильтра, то формулы (5.5) и (5.13) совпадут.

 

Алгоритм RLS

В принципе, в процессе приема сигнала можно на каждом очередном шаге пересчиты­вать коэффициенты фильтра непосредствен­но по формуле (5.13), однако это связано с нео­правданно большими вычислительными зат­ратами. Действительно, размер матрицы U постоянно увеличивается и, кроме того, не­обходимо каждый раз заново вычислять об­ратную матрицу (UU^T) . Сократить вычислительные затраты мож­но, если заметить, что на каждом шаге к мат­рице U добавляется лишь один новый стол­бец, а к вектору d – один новый элемент. Это дает возможность организовать вычисления рекурсивно. Соответствующий алгоритм на­зывается рекурсивным методом наименьших квадратов (Recursive Least Square, RLS).

Подробный вывод формул, описывающих алгоритм RLS, можно найти, например, в [2, 3], здесь, cледуя [4], приведем лишь основные идеи. При использовании алгоритма RLS производится рекурсивное обновление оценки обратной корреляционной матрицы P= (UU^T) , а вы­вод формул основывается на следующем мат­ричном тождестве:

(A + BCD) =

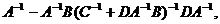
где А и С – квадратные невырожденные матрицы (необязательно одинаковых разме­ров), а В и D – матрицы совместимых раз­меров. Применение этой формулы для рекурсив­ного обновления обратной корреляционной матрицы Р  в сочетании с исходной формулой (5.13) для коэффициентов оптимального филь­тра дает следующую последовательность ша­гов адаптивного алгоритма RLS.

 

1. При поступлении новых входных данных u(k) производится фильтрация сигнала с использованием текущих коэффициентов фильтра w(k-1) и вычисление величины ошибки воспроизведения образцового сиг­нала:

                   y(k)=u (k)w(k-1);                                                                                              (5.14)

e(k) = d(k)-y(k).

2. Рассчитывается вектор-столбец ко­эффициентов усиления (следует отметить, что знаменатель дроби в следующих двух фор­мулах является скаляром, а не матрицей):

K(k) = 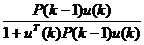.               (5.15)

3. Производится обновление оценки об­ратной корреляционной матрицы сигнала:

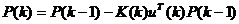.                (5.16)

4. Наконец, производится обновление коэффициентов фильтра

.                   (5.17)

Начальное значение вектора w обычно принимается нулевым, а в качестве исходной оценки матрицы Р используется диагональ­ная матрица вида CE , где скаляр С >>1 (в [2] рекомендуется С >=100).

В критериях ошибок (5.10) и (5.12) значениям ошибки на всех временных тактах придается одина­ковый вес. В результате, если статистичес­кие свойства входного сигнала со временем изменяются, это приводит к ухудшению каче­ства фильтрации. Чтобы дать фильтру возмож­ность отслеживать нестационарный входной сигнал, можно применить в (5.10) экспоненци­альное забывание, при котором вес прошлых значений сигнала ошибки экспоненциально уменьшается

.

В этом случае формулы (15), (16) принимают следующий вид

;

.

Главным достоинством алгоритма RLS яв­ляется быстрая сходимость. Однако достига­ется это за счет значительно более высокой (по сравнению с алгоритмом LMS) вычисли­тельной сложности. Согласно [2] при опти­мальной организации вычислений для обнов­ления коэффициентов фильтра на каждом так­те требуется (2.5N²+4N) пар операций «умножение–сложение».

 

Алгоритм Кальмана

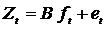                                                   (3.1)

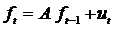
Прежде чем рассматривать применение алгоритма Кальмана для решения задачи адап­тивной фильтрации, напомним формулировку задачи фильтрации случайного процесса с известными динамическими свойствами, для решения которой фильтр Кальмана изначаль­но предназначен. Цель фильтра Кальмана – минимизировать дисперсию оценки вектор­ного дискретного случайного процесса х(k), изменяюще­гося во времени следующим образом:

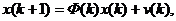
где Ф(k) – матрица перехода, v(k) –слу­чайный вектор (шум процесса), имеющий нор­мальное распределение с корреляционной матрицей .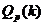

Для наблюдения доступен линейно преоб­разованный процесс у(k), к которому добав­ляется шум наблюдения

,

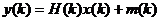где Н(k) – матрица наблюдения, m(k) – шум наблюдения, представляющий собой слу­чайный вектор, имеющий нормальное распре­деление с корреляционной матрицей Q_m(k).

Поиск алгоритма для рекурсивного об­новления оценки процесса 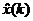дает следу­ющую последовательность формул:

 – прогнозируе­мое значение наблюдаемого сигнала;

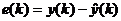  – невязка между про­гнозируемым и реально наблюдаемым значе­ниями;

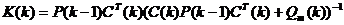 – кальмановский коэффициент усиления;

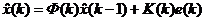 – обновление оценки процесса ;

 – обновление оценки корреляционной матрицы ошибок фильтрации.

При использовании фильтра Кальмана для решения задачи адаптивной фильтрации от­слеживаемым процессом является вектор коэффициентов оптимального фильтра w.

Предположим, что детерминированных из­менений коэффициентов не происходит, по­этому матрица перехода Ф является еди­ничной: Ф(k) = E. В качестве матрицы наблю­дения выступает вектор содержимого линии задержки фильтра u(k). Таким образом, вы­ходной сигнал фильтра представляет собой прогнозируемое значение наблюдаемого сигнала, а в качестве самого наблюдаемого сигнала выступает образцовый сигнал адап­тивного фильтра d(k). Шум наблюдения в данном случае является ошибкой воспроиз­ведения образцового сигнала, а матрица Q  превращается в скалярный параметр – средний квадрат сигнала ошибки. Как отме­чается в [3], величина этого параметра сла­бо влияет на поведение алгоритма. Рекомен­дуемые значения – (0.001...0.01) .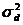

Если фильтруется стационарный случай­ный процесс, коэффициенты оптимального фильтра являются постоянными и можно при­нять Q 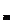 = 0. Чтобы дать фильтру возмож­ность отслеживать медленные изменения статистики входного сигнала, в качестве Q  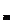может использоваться диагональная матрица.

В результате приведенные выше формулы принимают следующий вид

y(k)=u (k) 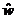(k - 1) – выходной сигнал фильтра (прогнозируемое значение образцо­вого сигнала);

e(k) = d(k)-y(k) – ошибка фильтрации;

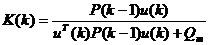 – кальмановский коэффициент усиления;

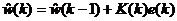  – обновление оценки коэффициентов фильтра w(k);

 – обновление оценки корреляционной матрицы ошибок оценивания.

Начальное значение вектора w обычно принимается нулевым, а в качестве исходной оценки матри­цы Р используется диагональная матрица вида CЕ, где Е – единичная матрица.

Сравнивая формулы, описываю­щие алгоритмы RLS и Кальмана, лег­ко заметить их сходство [7]. Вычислительная сложность и качественные парамет­ры двух алгоритмов также оказываются весь­ма близкими. Разница заключается лишь в ис­ходных посылках, использовавшихся при вы­воде формул, и в трактовке параметров алго­ритмов. В некоторых источниках алгоритмы RLS и Кальмана применительно к адаптивной фильтрации отождествляются.