2018-02-14
4163
Разумеется, нередко встречаются ситуации, несводимые к уравнению линейной регрессии, пожалуй, самым распространенным таким случаем является ситуация, когда между объясняемой и объясняющей переменной наблюдается квадратичная зависимость. Рассмотрим этот вариант.
Вполне аналогично случаю линейной зависимости, мы располагаем на старте некоторыми наборами значений {xi,yi} (или геометрически – набором точек {Pi}). При этом как минимум одна переменная yi содержит случайную составляющую ui. Поэтому точная запись нашего соотношения будет иметь вид:
yi = b1 + b2 xi + b3 xi2 + ui (2.12)
Вполне аналогично линейной ситуации, наша цель провести на плоскости (X,Y) параболу таким образом, чтобы она была максимально близка к нашему набору точек.
Пусть уравнение такой параболы имеет вид: 
– здесь мы через 
обозначили значения на модельной параболе.
Как только мы проведем любую параболу, у нас в каждой точке появятся отклонения εi = yi – , наша задача состоит теперь в том, чтобы так подобрать коэффициенты модели b1, b2 и b3, чтобы минимизировать отклонения в совокупности; используя МНК мы будем стремиться минимизировать сумму квадратов отклонений εi.
Соответственно получим задачу:
(2.13)
Чтобы найти оптимальные значения искомых параметров регрессии 
следует продифференцировать функцию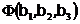 
по этим трем переменным и каждую из производных приравнять нулю – получим следующую систему трех уравнений с тремя неизвестными:
(2.14 а)
(2.14 б)
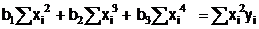(2.14 в)
Нетрудно обнаружить, что, несмотря на видимую сложность, система организована очень закономерно. Степень иксов, которые суммируются для вычисления коэффициентов системы вырастает на единицу при смещении на единицу сверху вниз (в первом уравнении первый коэффициент и правая часть содержат переменную x в нулевой степени, суммирование этих единиц и породило коэффициент (1,1), равный n).
В отличие от линейного случая, общее решение системы (2.14) имеет слишком сложный вид, неудобный как для записи, так и для непосредственных вычислений. Обычно просто вычисляют коэффициенты системы как числа, а потом решают получившуюся систему методом Гаусса.
Общую схему решения задачи квадратичной регрессии можно представить в виде следующей таблицы:
| xi | yi | xi2 | xi3 | xi4 | xi yi | xi2 yi |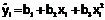 
| εi |
| x1 | y1 | x12 | x13 | x14 | x1 y1 | x12 y1 |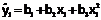 
| ε1 = y1– 
|
| x2 | y2 | x22 | x23 | x24 | x1 y1 | x12 y1 |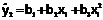 
| ε2 = y2– 
|
| … | … | … | … | … | … | … | … | … |
| xn | yn | xn2 | xn3 | xn4 | xn yn | xn2 yn | 
| εn =yn– 
|
| 
| 
| 
| 
| 
| 
| 
|
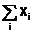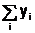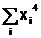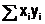Используя исходные данные заполняем первые два столбца таблицы. Потом вычисляем и заполняем следующие пять столбцов. Далее, для первых семи столбцов вычисляем элементы последней строки: суммы по столбцам.
Теперь мы располагаем всеми коэффициентами и правыми частями системы уравнений (2.14) и можем ее решить. Решая систему, находим набор неизвестных коэффициентов квадратичного уравнения регрессии b1, b2 и b3.
Теперь, зная все коэффициенты, мы можем вычислить все значения , после этого вычисляем отклонения εi и вычисляем величину стандартной ошибки аппроксимации σ.
[1] Это т.н. статистическое определение вероятности по сути представляет собой одну из форм закона больших чисел.
[2] Здесь и далее вариантой называется одно конкретное значение случайной величины полученное в результате опыта.
[3] Согласно Плутарху, солдаты двух легионов, бежавшие от Спартака, бросив оружие, были подвергнуты децимации по распоряжению Марка Красса
[4] От английского random – случайный (отсюда: рандомизация – «ослучайнивание»).
[5] Музыка на CD-диске записана в цифровом формате. Громкость звука имеет обычно двухбайтовое представление, т.е. может принимать примерно 65 000 различных дискретных значений, мы на слух не замечаем того факта, что амплитуда записана дискретно.
[6] Некоторые методы обработки данных требуют определенного минимального числа вариант в группе, например не менее 5-ти для применения метода χ-квадрат (см. далее).
[7] О вычислении см. ниже.
[8] Напомним, что для вычисления вероятности попадания нормально распределенной случайной величины в интервал (а, b) необходимо пересчитать этот интервал в нормированный интервал (a, b) по формулам: , после чего искомая вероятность вычисляется по формуле Р = Ф(b) – Ф(a). При таком преобразовании точка µ–σ превращается в (–1), а точка µ+σ превращается в +1; вообще, точка µ–сσ превращается просто в –с, а точка µ+сσ соответственно просто в с.
[9] Обратите внимание, вопрос поставлен именно так «можно ли считать?», а не «является ли?», это объясняется как раз тем, что мы можем утверждать «у нас нет оснований отвергнуть нулевую гипотезу», но не можем утверждать «тем самым мы доказали, что».
[10] Т.е. полученные в результате обработки данных наблюдений.
[11] Число степеней свободы для данного типа распределения определяется как число интервалов классификации k минус число параметров, которые необходимо задать, чтобы вычислить величины для данного распределения. Для нормального распределения необходимо задать 3 таких параметра: N, и σ. Потому для нормального распределения формула и принимает вид: f = k – 3, для биномиального и экспоненциального распределений достаточно задать два параметра: N и, потому для них формула примет вид: f = k – 2.
[12] Например, можно считать, что {xi} и {yj} это список размеров и ростов верхней одежды, а опыт состоит в подборе этих параметров для одного человека.
[13] Т.е. матожидание этих оценок не совпадает с оцениваемой величиной
[14] Напомним, что запись M[...] означает математическое ожидание для выражения (...).
[15] Напомним, что здесь как обычно символ означает дисперсию случайной величины Х.
[16] Нетрудно заметить, что в выражении для коэффициента корреляции множитель входит и в числитель и в знаменатель и, следовательно, сокращается. Теперь если интерпретировать величины и как координаты соответствующих векторов, то получится, что Cov(x,y) есть скалярное произведение этих векторов, а есть произведение их длин. Тогда получим, что выражение превращается в известную формулу для косинуса угла между векторами:.
Разумеется, отсюда вытекает, что возможные значения коэффициента корреляции принадлежат отрезку [–1, 1]
[17] Обратите внимание: при использовании критерия Фишера, как и при использовании параметра, в качестве нулевой гипотезы принимается гипотеза о случайности совпадений, а не о случайности различий. Соответственно, чем больше значение параметра критерия F, тем вероятнее, что наблюдаемая близость между объясняемыми величинами yi и модельными величинами носит не случайный, а закономерный характер. Чем больше величина критерия, тем больше наша уверенность в адекватности найденного уравнения.
[18] Напомним, что здесь b2 гипотетический, а - полученный из уравнения регрессии коэффициент пропорциональности между объясняемой и объясняющей переменными.
[19] Функции такого типа также широко используются как модели производственных функций (функция Кобба-Дугласа для одной инструментальной переменной).
[20] Строгая монотонность f(X) необходима для того, чтобы связь между двумя объясняющими переменными: исходной X и модифицированной Z= f(X) – была взаимно однозначной; каждому значению X соответствует одно и только одно значение Z. И обратно: каждому значению Z соответствует одно и только одно значение X.
