Напомним, что при вычислении коэффициентов регрессии мы исходим из предположения, что в каждом наблюдении величина yj состоит из двух компонент: 1)неслучайной составляющей b1 + b2 xi и 2)случайного члена ui: yi = b1 + b2 xi + ui (2.1).
В результате мы получаем представление случайной величины Y в виде  , причем
, причем  . Заметим, что в силу предположения о наличии случайной составляющей u в составе величины Y, найденные нами коэффициенты регрессии
. Заметим, что в силу предположения о наличии случайной составляющей u в составе величины Y, найденные нами коэффициенты регрессии  тоже являются случайными величинами. Соответственно, возникает задача оценить стандартные ошибки для этих случайных величин, построить доверительные интервалы и т.п.
тоже являются случайными величинами. Соответственно, возникает задача оценить стандартные ошибки для этих случайных величин, построить доверительные интервалы и т.п.
Если исходить из того, что нам известна дисперсия  случайной составляющей u в составе величины Y, то для вычисления величин стандартных отклонений коэффициентов регрессии можно получить следующие выражения:
случайной составляющей u в составе величины Y, то для вычисления величин стандартных отклонений коэффициентов регрессии можно получить следующие выражения:
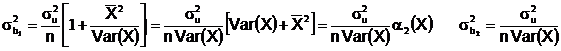 (2.10)
(2.10)
Из приведенных выражений следуют очевидные заключения.
Во-первых, дисперсии коэффициентов регрессии обратно пропорциональны количеству наблюдений в выборке.
Во-вторых, дисперсии коэффициентов прямо пропорциональны дисперсии случайного члена и обратно пропорциональны дисперсии Х. Дело в том, что наблюдаемые изменения величины Y отчасти вызваны изменениями Х, а отчасти случайным членом u. И чем меньше вариация Х, тем большая доля в изменении объясняемой величины порождена именно случайным членом; соответственно тем больше будет и дисперсия коэффициентов регрессии. Как видим, важны не абсолютные значения величин  и Var(X), а их отношение: чем оно больше, тем большая доля в изменении Y порождена случайными причинами. Соответственно, тем большей окажется и дисперсия коэффициентов регрессии.
и Var(X), а их отношение: чем оно больше, тем большая доля в изменении Y порождена случайными причинами. Соответственно, тем большей окажется и дисперсия коэффициентов регрессии.
В реальной ситуации мы разумеется не можем знать величину  , но мы можем построить ее оценку. Если мы провели прямую регрессии, значит нам уже известны величины εi = yi –
, но мы можем построить ее оценку. Если мы провели прямую регрессии, значит нам уже известны величины εi = yi –  , следовательно мы можем вычислить вариацию Var(ε). Тогда несмещенная оценка дисперсии случайного члена u примет вид:
, следовательно мы можем вычислить вариацию Var(ε). Тогда несмещенная оценка дисперсии случайного члена u примет вид:
 (2.11)
(2.11)
При этом вариацию Var(ε) следует умножить на корректирующий множитель  , т.к. число степеней свободы при вычислении характеристик коэффициентов линейной регрессии составляет n–2 (мы уже знаем два коэффициента).
, т.к. число степеней свободы при вычислении характеристик коэффициентов линейной регрессии составляет n–2 (мы уже знаем два коэффициента).
Теперь располагая оценкой (2.11) мы можем получить несмещенные оценки дисперсии коэффициентов регрессии:
 (2.12)
(2.12)
где 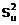 вычисляется по формуле (2.11). Корни квадратные из величин
вычисляется по формуле (2.11). Корни квадратные из величин  и
и 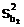 называются стандартными отклонениями коэффициентов регрессии:
называются стандартными отклонениями коэффициентов регрессии:
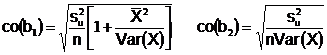 (2.13)
(2.13)
 2018-02-14
2018-02-14 342
342








