Тема 4. Обобщенный метод наименьших квадратов

1 2 3 4 5 6 7

4.1 Сущность метода

4.2 Применение метода в корреляционном и регрессионном анализе

4.3 Оценка полученной модели и пример

4.1 Сущность метода

Имеется простейший вид линейной зависимости:

у=а+b*х, где а - пересечение (intersept)

b – угол наклона (stop)

где: а,b – постоянные коэффициенты, которые определяются методом наименьших квадратов. По этому методу рассчитывается и находится минимум суммы квадратов отклонений фактических значений y от вычисленных по уравнению прямой:

y_факт– y_рас)²® min

y_рас.= a+bx_факт

подставив в предыдущее

y_факт-а-bх_факт)²® min

в этом уровне неизвестны только а и b, а известны y_фи x_фми

Для отыскания минимума частные производные по а и b приравниваются к 0:

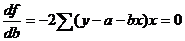
После преобразований:

Система решается относительно коэффициентов «а» и «в», т.е. в результате получаются их численные значения.

4.2 Применение метода в корреляционном и регрессионном анализе

4.2.1.МНОГОФАКТОРНЫЙ КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ

Цели: Изучение характера и степени влияния на моделируемый показатель отдельных факторов; отбор наиболее существенных факторов; получение количественной оценки зависимости.

Регрессионная модель имеет вид:

y=f(x1, x2, …, xn)

где y – исследуемый экономический показатель, фвктор-функыя,

x1… xn – факторы-аргументы (независимые переменные).

Первичная статистическая обработка.

Для выявления степени влияния на функцию каждого фактора рассчитывают частные коэффициенты корреляции, очищенные от влияния всех других факторов:

Параметры a0…an определяются по методу наименьших квадратов из условия:

y_i – фактические значения исследуемого показателя;

_-расчетные значение структурных коэффициентов.

Коэффициент множественной корреляции отражает совокупное влияние нескольких факторов на изменения результативного признака. Значение его может быть от нуля до единицы со знаком минус или плюс:

-1<=R<=1; если R=0 - связь отсутствует, если R=1 – связь функциональная.

Для двух факторов:

;

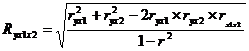n факторов:

R_xy1x2…xn=

где - стандартизированный коэффициент регрессии:

4.3 Оценка полученной модели и пример

Существенность коэффициента кореляции R проверяется по критерию Фишера

Расчетное значение F должно быть больше табличного, тогда коэффициент связи существенен.

Для сравнения с табличным необходимо иметь заданный уровень значения (5%)ْ и расчитать число степеней свободы.

V1= (число факторов (N))

V2= n-N-1 (число наблюдений- число факторов – 1)

В случаи нелинейной формы связи для оценки степени ее тесноты используют множественное корреляционное отношение:

Значимость по t-критерию Стьюдента с V=n-N-1

где -среднеквадратичная ошибка множественного корреляционного отношенияْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْْ:

Коэффициент множественной детерминации R² показывает, на сколько процентов вариация изменения показателя определяется вариацией изменениям включенных в модель факторов.

При предварительной обработки исходной статистической информации по каждому из включенных показателей определяется среднее значение, дисперсия, среднее квадратичное отклонение, коэффициент вариации коэффициент парной корреляции, а также расхождение между фактическим значением и средней.

Например:

Главки	Ед.изм	у min	у max	у ср.	*у	Vy
Укртепломонтаж		13.4	16.8	14,8	1,4	9,6	min
Укрметаллургмонтаж		12,2	13,9	12,9	0,6	4,9
Главцентрмонтаж		10,7	13,4	11,8	0,89	7,5
Главхиммонтаж		9,85	11,7	10,9	0,63	2,6	max
Укрстальконструкция		12,09	15,9	14,6	1,27	8,6

Разброс показателей выработки на одного работника (у) определяется коэффициентом вариации.

Колебания коэффициента вариации Vy свидетельствуют о наличии резервов роста производительности труда.

Факторы производительности труда в строительстве

Факторы	Средние			Vу	К.К.
У	99.3	4.9	24.6	4.9
Х1	4.5	1.0	1.08	22.9	0.13
Х2	4.57	3.4	10.16	74.5	0.548
Х3	9.3	4.04	16.3	23.2	0.38
Х4	0.24	0.1	0.01	42.2	0.28
Х5	92	16.8	28.2	18.2	0.31
Х6	17.6	10.6	106.1	60.2	0.45