Методические указания

В экономике широко используются методы статистики. Ставя цель дать количественное описание взаимосвязей между экономическими переменными, эконометрика, прежде всего, связана с методами регрессии и корреляции.

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Парная регрессия – уравнение связи двух переменных y и x:

где y – зависимая переменная (результативный признак),

х – независимая, объясняющая переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Линейная регрессия:

Нелинейные регрессии делятся на два класса:

· регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам,

· регрессии, нелинейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

· Полиномы разных степеней

· Равносторонняя гипербола

Регрессии, нелинейные по оцениваемым параметрам:

· Степенная

· Показательная

· Экспоненциальная

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических минимальна:

Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина y складывается из двух слагаемых:

где y – фактическое значение результативного признака; – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; e – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина e называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака , подходят к фактическим данным y.

К ошибкам спецификации относятся неправильный выбор той или иной математической функции для и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_xy и индекс корреляции r_xy. Для линейной регрессии (), причем, если коэффициент регрессии то и, наоборот, при

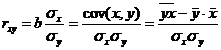
Оценку качества построенной модели дает коэффициент детерминации, а также средняя ошибка аппроксимации.

Коэффициент детерминации (квадрат линейного коэффициента корреляции ) характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака:

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических.

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. y и . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака по каждому наблюдению представляет собой ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:

Допустимый предел значений 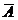- не более 8-10% (это свидетельствует о хорошем подборе модели к исходным данным).

Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения:

Оценка значимости уравнения регрессии в целом дается с помощью F‑критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т.е. b=0, и, следовательно, фактор x не оказывает влияния на результат y.

Непосредственному расчету F ‑критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной y от среднего значения на две части: «объясненную» и «необъясненную»:

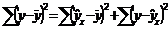
где – общая сумма квадратов отклонений;

- сумма квадратов отклонений, обусловленная регрессией (объясненная или факторная);

- остаточная сумма квадратов отклонений (необъясненная).

Если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор x оказывает существенное влияния на результат y. Это равносильно тому, что коэффициент будет приближаться к единице.

При расчете объясненной суммы квадратов 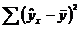используются теоретические (расчетные) результативного признака 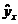, найденные по линии регрессии:

Сумма квадратов отклонений, обусловленных линейной регрессией, составляет:

Поскольку при заданном объеме наблюдений по x и y факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы. Число степеней свободы – это число свободы независимого варьирования признака; оно связано с числом единиц совокупности n и с числом определяемых по ней констант. Существует равенство между числом степеней свободы общей, факторной и остаточной суммы квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n-2. Число степеней для общей суммы квадратов составляет n-1, так как для требуется n-1 независимых отклонений (из n единиц после расчета среднего уровня свободно варьируются лишь n-1, число отклонений).

Следовательно, имеем два равенства:

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F ‑критерия для проверки нулевой гипотезы :

Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Фактическое значение F -критерия Фишера сравнивается с табличным значением при уровне значимости a и степенях свободы k₁=m и k₂=n-m-1.

Табличное значение F ‑критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F ‑критерия признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: . H₀ отклоняется.

Если же величина окажется меньше табличной , то вероятность нулевой гипотезы выше заданного уровня (например, 0.05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым, H₀ не отклоняется.