2018-02-14
765
Из определения энтропии (8.41) и первого начала термодинамики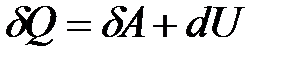 
получим:
.
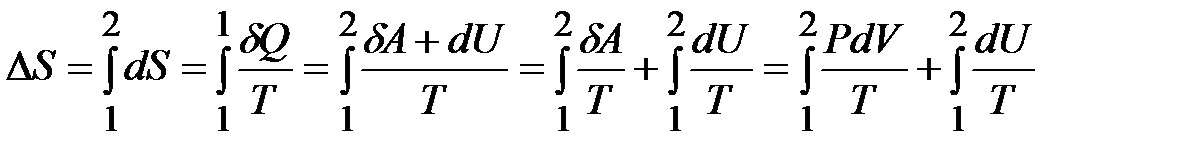Далее, из уравнения Менделеева-Клапейрона следует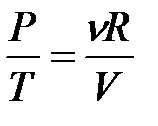 
; а приращение внутренней энергии идеального газа равно 
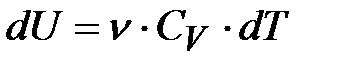, тогда
,
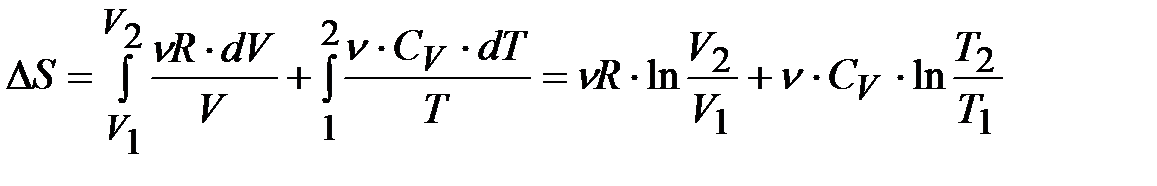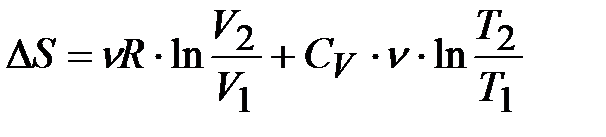. (8.47)
Из (8.47) видно, что энтропия увеличивается при расширении газа и при его нагревании.
Для изохорного процесса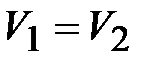 
, тогда 
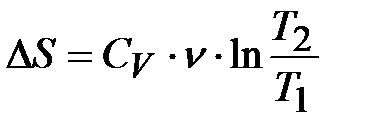. Также для изохорного процесса 
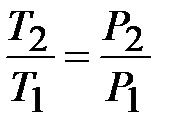, следовательно,
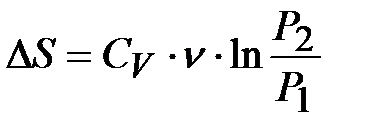. (8.48)
Для изобарного процесса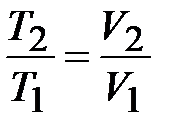 
, и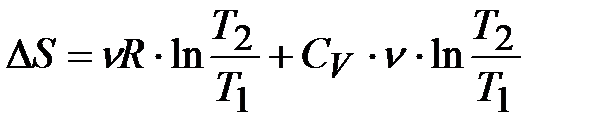 
. Воспользуемся уравнением Майера: 
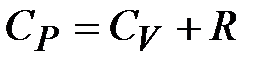, тогда
,
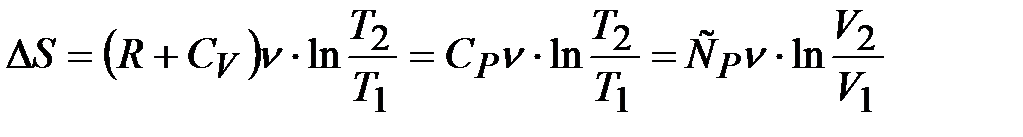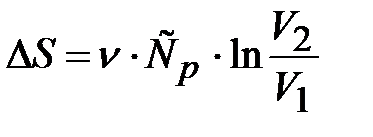. (8.49)
Для изотермического процесса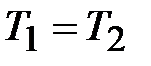 
, 
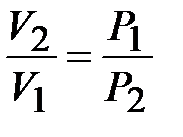, тогда
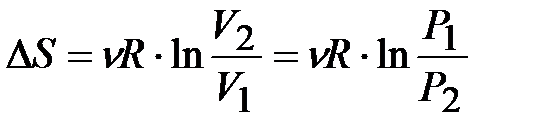. (8.50)
При адиабатическом процессе нет теплообмена системы с окружающей средой, и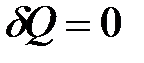 
, тогда по определению (8.41) 
.
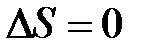В таблице 8.1 систематизированы все полученные результаты для изменений термодинамических величин при обратимых изопроцессах с идеальным газом; здесь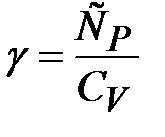 
– показатель Пуассона.
Билет
Вынужденные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс.
Для того, чтобы колебания не затухали, колебательную систему нужно подпитывать энергией; например, с помощью периодически действующей вынуждающей силы (4.37).
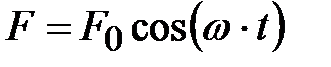. (4.37)
По второму закону Ньютона: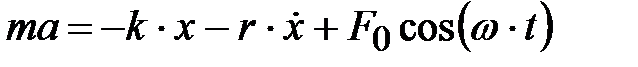 
; или
, 
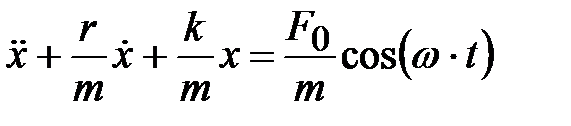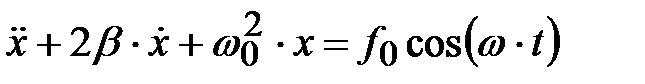, (4.38)
где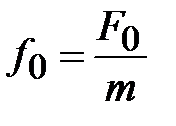 
. Уравнение (4.38) – дифференциальное уравнение вынужденных колебаний. Его решение (без доказательства):
,
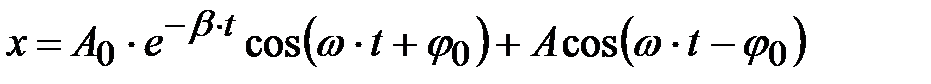причём первое слагаемое при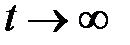 
затухает и для установившихся колебаний
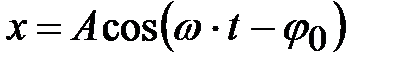. (4.39)
Амплитуда вышужденных колебаний в (4.39) зависит от частоты:
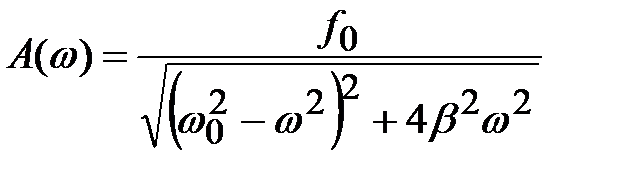(4.40)
Начальная фаза:
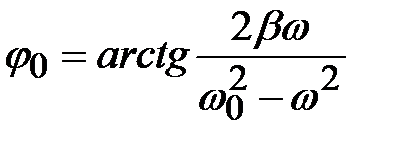. (4.41)
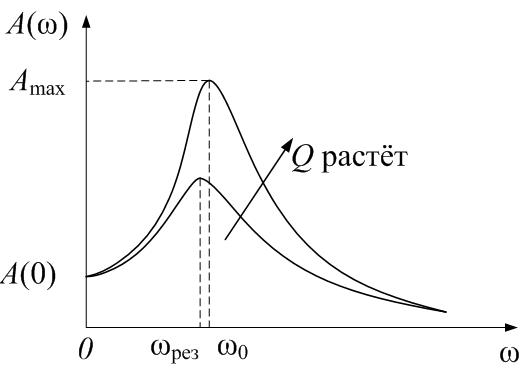
На рис. 4.14 дан график функции (4.40); это – резонансные кривые.
| Рис.4.14 |
Если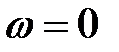 
, то статическое смещение 
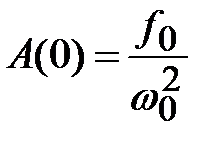. При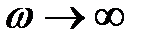 
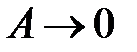. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний системы (резонансной частоте) называется резонансом. Найдём резонансную частоту. Амплитуда максимальна, если подкоренное выражение в знаменателе (4.40) минимально, то есть
;
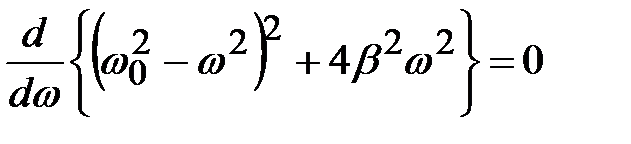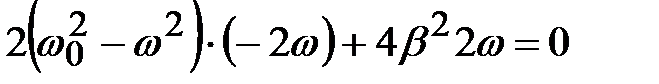; (4.42)
;
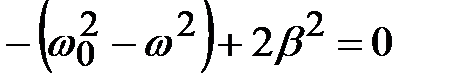откуда
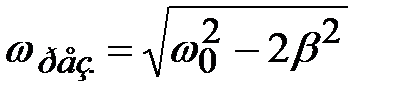. (4.43)
Значение 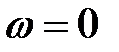– тоже решение уравнения (4.42), но это – минимум. Если же выполняется (4.43), амплитуда вынужденных колебаний максимальна и равна
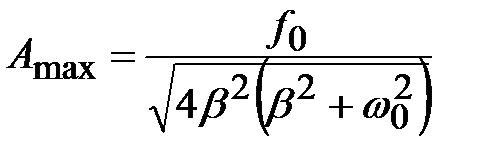. При условии малости затухания (
):
;
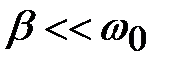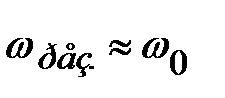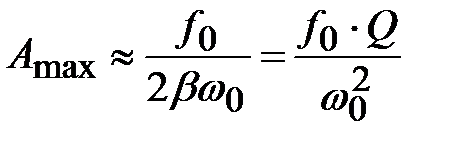. (4.44)
