Затухающие колебания

На реальную колебательную систему, кроме упругой (квазиупругой) силы

,                                             (4.8)

действует сила сопротивления среды . При малых скоростях можно считать пропорциональной скорости движения, а направление её противоположно скорости:

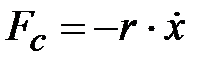,                                                (4.23)

здесь r – коэффициент сопротивления среды,  – скорость движения.

По второму закону Ньютона: ; с учетом того, что , получим дифференциальное уравнение свободных затухающих колебаний:

,                        (4.24)

Здесь приняты следующие обозначения:

,                                             (4.25)

,                                              (4.26)

где β – коэффициент затухания,  – циклическая частота собственных колебаний, то есть колебаний системы, если бы затухания не было.

Решением дифференциального уравнения (4.24) при условии малости затухания (то есть если β < ω₀) является функция

,                                    (4.27)

в чем можно убедиться путем подстановки (4.27) в (4.24), предварительно найдя производные. При этом будет получено и выражение для круговой частоты и периода затухающих колебаний:

;    .           (4.28)

График функции (4.27) приведен на рис.4.12. Если затухание велико (β>ω₀), движение системы не имеет колебательного характера и будет апериодическим (рис.4.13). Этот случай в дальнейшем рассматриваться не будет.

Рис.4.13

Рис.4.12

Таким образом, если на тело, кроме силы упругости, действует сила сопротивления среды, то тело будет совершать колебательное (но не гармоническое) движение с частотой, зависящей от массы тела m, жесткости пружины k и коэффициента затухания β, характеризующего силу сопротивления среды. При этом частота ω затухающих колебаний оказывается меньше частоты  собственных незатухающих колебаний из-за действия тормозящей силы сопротивления. Амплитуда колебаний будет с течением времени уменьшаться по экспоненциальному закону:

,                                           (4.29)

где  – начальная амплитуда колебаний. Быстроту затухания колебаний характеризует логарифмический декремент затуханияλ. Логарифмический декремент затухания – это натуральный логарифм отношения амплитуд двух следующих друг за другом колебаний, то есть амплитуд колебаний в моменты времени t и (t+T):

,                                          (4.30)

;

.                                                (4.31)

Введём время релаксации:

;                                                   (4.32)

Тогда при :

,

то есть за время релаксации амплитуда уменьшается в е раз. Число колебаний за время релаксации равно

.                                (4.33)

Еще одна важная физическая величина характеризует затухание колебаний – добротность:

.                                               (4.34)

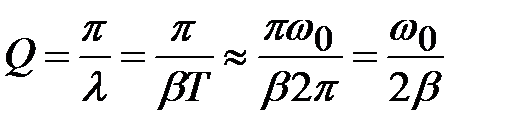
              ,                  (4.35)                           

при условии малости затухания: .

Добротность пропорциональна числу колебаний за время релаксации (4.33), (4.34):

.                                             (4.35)

Можно показать, что добротность обратно пропорциональна относительной убыли энергии колебаний за время, равное одному периоду:

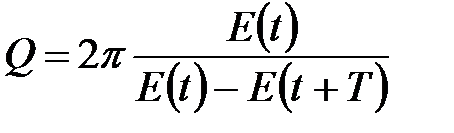.                                  (4.36)