Расчётно-графическое задание № 2

Вычисление определенных интегралов

Общие сведения

Задача численного интегрирования функции заключается в вычислении значения определенных интегралов на основании ряда значений подынтегральной функции f (x) в точках x 0, x 1,… xn –1, xn, которые называются узлами интерполяции. Если f (xi) – значения подынтегральной функции в узлах интерполяции, то

.                (1)

                                                           

Сумма, стоящая в правой части выражения (1), называется квадратурной суммой, а само выражение вида (1) – формулой механических квадратур. Для построения квадратурных сумм заданную функцию f (x)заменяют интерполирующим полиномом P_n (x) степени не выше n и принимающим в узлах интерполяции те же значения, что и f (x), т.е.

P_n (x ₀)= f (x ₀)= y ₀, P_n (x ₁)= f (x ₁)= y ₁ ,…P_n (x_n)= f (x_n)= y_n.    (2)

В качестве интерполирующих полиномов чаще всего выбираются полиномы Лагранжа и Лежандра.

Квадратурные формулы Ньютона – Котеса

Эти формулы относятся к случаю равноотстоящих узлов интерполяции, т.е при выбранном шаге интерполяции h= (b–a)/ n, отрезок [a, b] разбивается с помощью равноотстоящих точек x ₀ =a, x_i=x ₀ +ih, (i= 1 ,….,n– 1), x_n=b на n равных частей.

В качестве интерполирующего полинома берется полином Лагранжа. Квадратурная формула (4.1) при этом принимает вид

,         (3)

где                 (4)                                                  

 – постоянные, называемые коэффициентами Котеса.

Нетрудно убедиться, что

Формула трапеций

При n =1 из (4) имеем: H₀ =1/2, H ₁=1/2.

Отсюда:

.                 (5)

Выражение (5) – это хорошо известная формула трапеций для приближенного вычисления определенного интеграла.

Если отрезок интегрирования [ a, b ] достаточно большой, то для вычисления интеграла 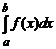 необходимо промежуток интегрирования разделить на k равных частей [ x ₀, x ₁], [ x ₁, x ₂],…., [ x_{k -1}, x_k ] и к каждой из них применить формулу трапеций. Введя обозначение f (x_i) =y_i, получим

,                 (6)                      

где h =(b – a)/(k · n).                                                            (7)                                                   

Геометрически формула (6) получается в результате замены графика подынтегральной функции ломаной линией.

 

Формула Симпсона

При n =2 из (4) получим: H ₀ = 1/6, H ₁ = 2/3, H ₂ = 1/6.

Так как x ₂ –x ₀ =2 h, то

.      (8)

Формула (8) носит название формулы Симпсона. Геометрически эта формула получается заменой кривой f (x) параболой, проходящей через три точки f (x ₀), f (x ₁) и f (x ₂) .

Для вычисления интеграла 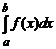, как и в случае формулы трапеции, промежуток интегрирования [ a, b ] разбивается на k равных частей и к каждой из этих частей применяется формула Симпсона, т.е. фактически число разбиений равно n·k =2 k. Таким образом, в методе Симпсона число разбиений должно быть четным. В результате получим:

    (9)

 

где y_i=f (x_i), i= 0, 1,…, 2 k, h = (b–a)/2 k.