Квадратурная формула Ньютона

При n =3 из (3) и (4) получим квадратурную формулу Ньютона:

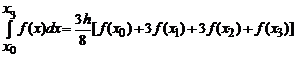,         (10)

 

которая иногда называется «правилом трех восьмых».

 Для распространения правила «трех восьмых» на интеграл 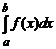 необходимо интервал [ a, b ] разбить nk =3 k равных частей, тогда:

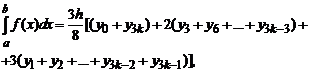  (11)

где y_i=f (x_i), i= 0, 1,…, 3 k, h = (b–a)/3 k.

Обратите внимание, что число разбиений кратно 3.

Четвертая формула Ньтона-Котеса.

Если n =4 и интервал [ a, b ] разбит на 4 k равных частей, то

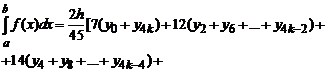
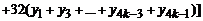.                               (12)

Формулы Ньютона-Котеса при больших n применяют редко. Обычно отрезок [ a, b ] разбивают на достаточно малые интервалы и к каждому из них применяют квадратурную формулу с малым n. В табл. 3 приведены значения коэффициентов Котеса для n от 1 до 8 в виде .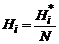

Таблица 3

n		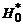		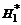		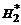		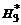		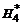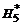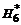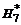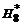N
1	1	1								2
2	1	4	1							6
3	1	3	3	1						8
4	7	32	12	32	7					90
5	19	75	50	50	75	19				288
6	41	216	27	272	27	216	41			840
7	751	3577	1323	2989	2989	1323	3577	751		17280
8	989	5888	–928	10496	–4540	10496	–928	5888	989	28350

На практике при вычислении определенных интегралов по формуле Ньютона-Котеса для любых значений n £ 8 нет необходимости вывода выражений, аналогичных (6), (9), (11) и (12). Следует просто промежуток интегрирования разделить на k равных частей и для каждой части, применив выбранную (заданную) квадратурную формулу, определить её площадь. После суммирования этих площадей Вы и получите значение интеграла. На этом пути Вам придется столкнуться с некоторыми трудностями как на этапе составления алгоритма, так и на этапе его реализации на языке C++. В чем они заключаются?

Пусть n =4, а k =2, т.е. промежуток интегрирования [ a, b ] делится на две равные части (рис. 1).

 

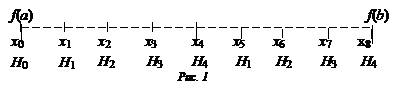Int = .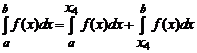

Применяя к каждому интегралу квадратурную формулу (3) для n =4, получим:

Int»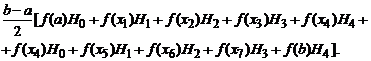

Так как Н ₀ =Н ₄, то

Int»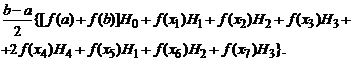

Распространим последнее выражение на случай произвольных n и k:

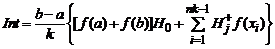,         (13)

 

где j = 1, 2,…, n,1, 2, …n, 1, 2,…;

.

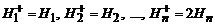Для реализации выражения (13) на языке C++ необходимо набор коэффициентов 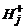 оформить в виде массива, не забывая, что индексы массива начинаются с нуля, а при j = [(i –1)% n ]·[ Н (i –1)% n)] индексы элементов этого массива будут меняться с нужной периодичностью, т.е. 0, 1, 2, …., n –1, 0, 1, 2, …., n –1, 0…

При решении практических задач оценка погрешностей квадратурной формулы Ньютона-Котеса (3) основана на двукратном вычислении интеграла на каждом шаге: вначале с шагом h (int1), а затем с шагом h /2 (int2). Если | int1–int2|<e, где e - заданная точность вычисления интеграла, то вычисления прекращаются и за искомое значение интеграла берут значение int2. В противном случае надо повторить расчет, увеличив количество разбиений k вдвое (т.е. ещё вдвое уменьшив шаг и т.д.). Такие программы с автоматическим определением шага в литературе называют адаптивными.