2018-02-14
481
Эта формула получена Гауссом при использовании интерполяционных полиномов Лежандра. Причем узлы интерполяции расположены неравномерно по отрезку интегрирования. Разделив отрезок интегрирования b–a на k равных частей и применив к каждой из них формулу Гаусса для фиксированного n, получим общую формулу Гаусса для вычисления определенного интеграла:
, (14)
где h= (b–a) /k – шагинтегрирования;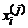 
– i -ая абсцисса j -ого шага интегрирования: x 0 -a, xj=xj- 1 +h, j= 1, 2,…, k; 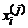= xj- 1 +Xih , i= 1, 2,…, n; Xi, Ai – абсциссы и коэффициенты формулы Гаусса, значения которых для n от 1 до 6 приведены в табл. 4.
Таблица 4
| n | i | Xi | Ai |
| 1 | 1 | 0,5 | 1,0 |
| 2 | 1 2 | 0,2113249 0,7886751 | 0,5 |
| 3 | 1 3 2 | 0,1127017 0,8872983 0,5 | 0,2777778 0,4444444 |
| 4 | 1 4 2 3 | 0,0694318 0,9305682 0,3300095 0,6699905 | 0,1739274 0,3260726 |
| 5 | 1 5 2 4 3 | 0,0469101 0,9530899 0,2307653 0,7692347 0,5 | 0,1184634 0,2393143 0,2844444 |
| 6 | 1 6 2 5 3 4 | 0,0337652 0,9662348 0,1693953 0,8306047 0,3806904 0,6193096 | 0,0856622 0,1803808 0,2339570 |
При n =1 квадратурная формула Гаусса (13) принимает самый простой вид:
, (15)
где h= (b–a)/ k; x 1 = a+ 0,5 h; xj = xj- 1 + h; yj = f (xj).
Выражение (15) носит название обобщенная формула прямоугольников. В этом случае интеграл равен сумме площадей прямоугольников, основания которых равны h, а высоты совпадают со значениями подынтегральной функции на середине элементарных участков интегрирования [ xj, xj +1].
При одинаковом числе ординат формула Гаусса дает большую точность, чем другие формулы, но она менее эффективна в методах с автоматическим выбором шага интегрирования. Это объясняется тем, что в формулах Ньютона-Котеса расстояния между узлами интегрирования одинаково и ординаты, вычисленные при шаге h, могут быть использованы и при половинном шаге. В формулах Гаусса это сделать нельзя, так как расстояния между абсциссами не одинаковы.
Метод рядов
Если подынтегральная функция f (x) разлагается в степенной ряд 
, равномерно сходящийся на интервале интегрирования [ a, b ], то интеграл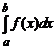 
может быть рассчитан на основании теоремы об интегрировании числового ряда:
.
Если ряд сходится достаточно быстро, то можно приближённо вычислить интеграл с помощью суммы конечного числа членов ряда.
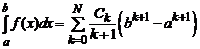. (16)
Выражения для коэффициентов Ck в разложении заданной подынтегральной функции f (x) в степенной ряд можно получить непосредственно или воспользоваться справочной литературой.
При использовании формулы (16) особое внимание следует обратить на задачу оценки погрешности вычисления, которая равна сумме отбрасываемых членов ряда (остатку ряда):
.
Наиболее просто оценить остаток знакопеременного ряда с монотонно убывающими по абсолютной величине членами, где он не превышает абсолютной величины первого из отбрасываемых членов на основании теоремы Лейбница. В подобной ситуации вычисление интеграла путём накопления суммы членов ряда прекращается именно тогда, когда модуль очередного члена ряда окажется меньше требуемой погрешности расчёта.
В случае знакопостоянных рядов проблема оценки усложняется. Найти сумму бесконечного числа отбрасываемых членов можно только в том случае, если они представляют собой геометрическую прогрессию вида 
, где q – знаменатель прогрессии. Если | q |<1, то, очевидно, погрешность вычисления равна сумме членов такого ряда:
. (17)
Однако совсем не обязательно, что остаток ряда образует именно геометрическую прогрессию, но иногда можно его члены свести к прогрессии, увеличивая (но не уменьшая) их. Если каждый член такой искусственно полученной прогрессии будет не меньше соответствующего члена ряда, из которого он получен, то следует ожидать, что сумма членов такой прогрессии, найденная по формуле (17), будет не меньше остатка ряда. Подобный искусственно подобранный оценочный ряд называется мажорирующим, а сам процесс – мажорированием.
Покажем, как используются подобные рассуждения на примере вычисления интеграла 
с точностью e=10-5. Разложим подынтегральную функцию в степенной ряд:
.
Поскольку отрезок интегрирования лежит внутри интервала сходимости (–1, 1), этот ряд можно почленно интегрировать.
.
Если ограничиться первыми N членами ряда 
, то для остатка будем иметь:
Основная идея последнего преобразования – заменить часть множителей в членах ряда [в данном случае 1/(2k+3)] одинаковой величиной, большей по значению 1/(2 N +3), тем самым превращая равенство в неравенство. Из неравенства 
при заданной погрешности e N =10-5 можно найти номер N =2, при котором e N =10-5<9.3×10-6.
Рассмотрим более общий случай, при котором подынтегральная функция разлагается в обобщенный степенной ряд 
, где 
– дробные числа, зависящие от номера k. Вычисляя интеграл в интервале сходимости путем почленного интегрирования, получаем
.
Оценим остаток ряда 
. Величины 
убывают. Заменяя их наибольшим значением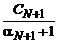 
, имеем 
. Далее в зависимости от конкретного ak ряды сворачивают, используя формулы для суммы бесконечно убывающей геометрической прогрессии.
Пример
Таким образом, для остатка ряда имеем 
. Задавая e N, можно найти число N удерживаемых членов, при котором остаток ряда не будет превышать заданную точность.
Задание
Составить программу вычисления определенного интеграла с автоматическим выбором шага интегрирования. Расчет интеграла различными методами, а также расчет подынтегральной и первообразной функции оформить в виде отдельных функций. Допустимую точность вычисления вводить в функции main() с клавиатуры. Функции, рассчитывающие интеграл, кроме значения интеграла должны возвращать и количество обращений к подынтегральной функции. Полученные численным методом значения интегралов необходимо сравнить с их значением, найденным через первообразную функцию.
*Для тех, кто претендует на автоматический зачет.
В программе вычисления интеграла по методу Симпсона изменить программу так, чтобы при вычислении интеграла с удвоенным количеством точек ни одна из ординат не вычислялась дважды.
Таблица 5
| Номер варианта | Вычисляемый Интеграл | Первообразная функция | Метод вычисления |
| 1 | 2 | 3 | 4 |
| 1 | 
|
| Формула Симпсона Формула Гаусса для n =4 |
| 2 | 
|
| Формула трапеций Метод рядов |
| 3 |
|
| Формула Симпсона Формула Ньютона-Котеса для n =5 |
| 4 |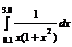 
|
| Формула Гаусса для n =2 Правило «трех восьмых» |
| 5 | 
|
| Формула трапеций Формула Гаусса для n =6 |
| 6* |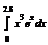 
|
| Формула Симпсона Метод рядов |
| 7 |
|
| Формула Ньютона-Котеса ля n =4 Формула Гаусса для n =5 |
| 8 | 
| 
| Формула Гаусса для n =4 Правило трех восьмых» |
Продолжение табл. 5
| 1 | 2 | 3 | 4 |
| 9 | 
|
 
| Формула Симпсона Формула Гаусса для n =5 |
| 10 |
|
| Формула Гаусса для n =4 Формула Ньютона-Котеса ля n =5 |
| 11 |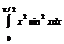 
| 
| Формула Гаусса для n =6 Правило «трех восьмых» |
| 12 | 
|
| Формулу Ньютона-Котеса для n =6 Формула трапеций |
| 13 |
|
| Формула Гаусса для n =5 Метод рядов |
| 14 | 
|
| Формула трапеций Формулу Ньютона-Котеса для n =4 |
| 15 |
|
| Правило «трех восьмых» Метод рядов |
Продолжение табл. 5
| 1 | 2 | 3 | 4 |
| 16 |
| 
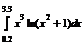
| Формула Гаусса для n =1 Формулу Ньютона-Котеса для n =7 |
| 17 | 
|
| Формула Симпсона Формула Гаусса для n =3 |
| 18 | 
|
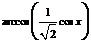
| Формула трапеций Формула Гаусса для n =2 |
| 19 |
|
| Формулу Ньютона-Котеса для n =4 Формула Гаусса для n =2 |
| 20 |
| 
| Формула Симпсона Формула Гаусса для n =5 |
| 21 | 
|
| Формула Симпсона Формула Гаусса для n =4 |
Окончание табл. 5
| 1 | 2 | 3 | 4 |
| 22 | 
| 
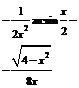
| Формулу Ньютона-Котеса для n =4 Формула Гаусса для n =3 |
| 23 | 
|
| Формула Симпсона Формулу Ньютона-Котеса для n =5 |
| 24 | 
|
| Формула Гаусса для n =3 Формула трапеций |
| 25 |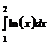 
|
| Метод рядов Формула Симпсона |
ИНФОРМАТИКА
