2018-02-14
6495
Задача 1.
Каким должен быть наименьший вес тела 2, для того чтобы тело 1 весом 200 Н начало скользить по горизонтальной плоскости, если коэффициент трения скольжения равен 0,6 (рис.71)?.
Задача 2.
Однородный брус АВ опирается в точке А на гладкую стену, а в точке В на негладкий пол. Определить наименьший коэффициент трения скольжения между брусом и полом, при котором брус останется в покое (рис.72).
 |
 |
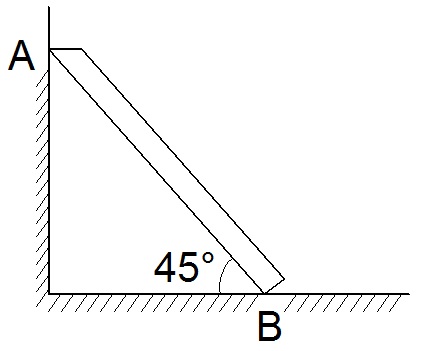Рис. 71 Рис. 72
Задача 3.
Каким должен быть вес тела 1, для того чтобы началось скольжение вверх по наклонной плоскости, если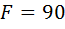 
Н, а коэффициент трения скольжения 
(рис.73)?
Задача 4.
 |
 |
(рис.74)?
Рис. 73 Рис. 74
Задача 5.
Электровоз поднимается по прямолинейному пути, имеющему уклон 0,008, с постоянной скоростью. Вес электровоза 12000 кН. Какова должна быть сила тяги электровоза Р, если сопротивление движению равно 0,005 силы давления электровоза на рельсы?
Задача 6.
 |
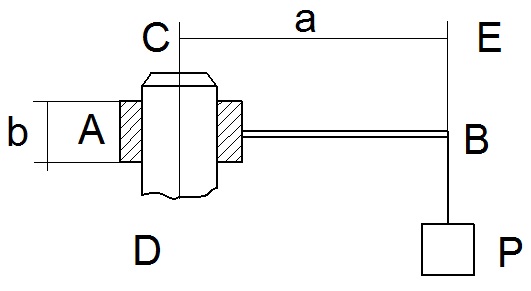(рис.75)?
Рис. 75
Трение качения
|
Рис 76 |
Тело, имеющее форму катка, под действием приложенных сил, может катиться по поверхности другого тела. При этом из-за деформации поверхностей этих тел, в месте их соприкосновения, могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса – колеса электровозов, вагонов, автомашин, шарики и ролики в подшипниках.
Соприкосновение катка с поверхностью вследствие деформации происходит по некоторой площадке.
При этом точка приложения нормальной реакции поверхности смещается так, что возникает пара сил (
), называемая парой сопротивления качению (рис. 76).
Величина плеча 
этой пары, зависящая от материала соприкасающихся тел, называется коэффициентом трения качения. Максимальная величина момента пары сил, препятствующей качению 
, определяется по формуле
,
где 
нормальная реакция плоскости, по которой катится тело.
В дальнейшем момент пары сил, препятствующей качению , будем называть моментом сопротивления качению.
Установим минимальное значение силы 
, необходимой для качения катка.
Предположим, что каток остается в покое. Тогда выполняются следующие уравнения равновесия:
; 
;
; 
;
; 
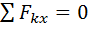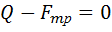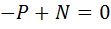Максимальная сила трения скольжения равна 
, тогда при равновесии катка из первого уравнения 
.
Из третьего уравнения минимальное значение силы , при котором каток еще остается в покое, равно 
.
При увеличении значения силы , возможны следующие случаи движения катка:
– каток катится без скольжения, это так называемый случай чистого качения;
– каток катится со скольжением.
Рассмотрим все эти три случая:
1. если 
, то при
а). 
– каток находится в покое;
в). 
– каток катится без скольжения;
с).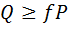 
– каток катится со скольжением.
2. если 
, то при
а). 
– каток находится в покое;
в). 
– каток скользит, не вращаясь, то есть каток движется поступательно;
с). 
– каток катится со скольжением.
Как правило, 
, то для начала качения катка требуется значительно меньшая сила , чем для начала его скольжения. Поэтому по мере увеличения силы каток сначала начинает катиться, а при дальнейшем ее увеличении к качению добавляется еще и скольжение.
Задача 1. При каких значениях угла наклона плоскости к горизонту, однородный цилиндрический каток радиуса
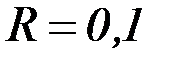м будет оставаться в покое, катиться без скольжения, катиться со скольжением. Коэффициент трения скольжения между плоскостью и катком 
, а коэффициент трения качения 
м (рис. 77)?
Рис. 77
Решение. На каток действуют силы тяжести 
, сила трения скольжения 
, момент сопротивления качению и нормальная реакция наклонной плоскости . Пусть каток остается в покое под действием этих сил, поэтому выполняются уравнения равновесия:
; 
;
; 
;
; 
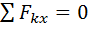Момент сопротивления качению равен .
1. Из второго уравнения 
, из третьего 
Тогда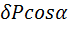 
= 
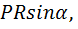отсюда 
Следовательно, равновесие сохранится для всех значений угла 
2. Из первого уравнения определим угол наклона плоскости, при котором каток будет катиться без скольжения. Максимальная сила трения скольжения равна 
, 
.
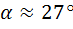Таким образом, при значении угла 
каток будет катиться без скольжения.
3. Если значение угла 
, то каток будет катиться со скольжением.
Проверим соответствие полученного решения неравенствам (1) или (2).
По условию задачи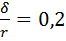 
, а 
, то есть выполняется соотношение (случай 1). При движении по наклонной плоскости сила, под действием которой каток приходит в движение, равна 
.
1. Предельное значение угла при равновесии равно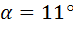 
, 
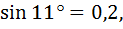тогда соотношение , 
, 
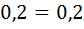выполняется и, следовательно, каток находится в покое.
2. При выполнении соотношения , каток катится без скольжения. Проверим, выполняется ли оно при изменении угла 
в пределах 
. Например,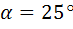 
, 
, 
. Тогда 0,5 
; 0,5 
. Второе неравенство из (1) выполняется, следовательно, каток катится без скольжения.
3. Третье неравенство из (1) 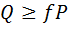должно выполняться при качении катка со скольжением. Пусть 
, 
. Тогда 
и 
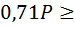0,5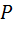 
; 
0,5. Неравенство тоже выполняется, следовательно, каток катится со скольжением.
Ответ: При 
каток остается в покое.
При 
каток катится без скольжения.
При , каток катится со скольжением.
 |
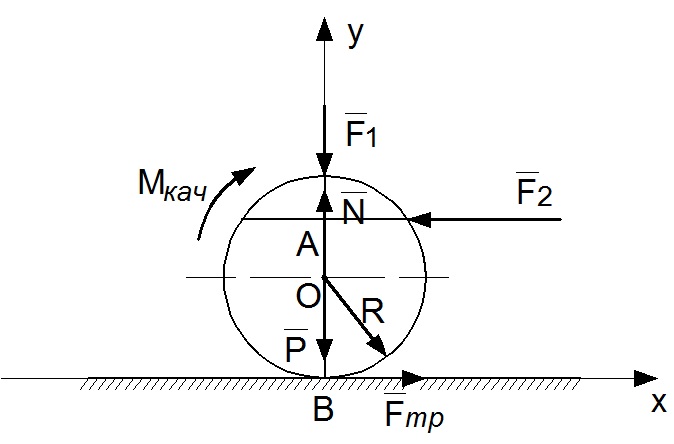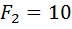Н и вертикальная 
. Каким должен быть наибольший модуль силы 
для того чтобы началось качение катка, если коэффициент трения качения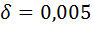 
м, радиус 
м, ОА=0,4 м (рис.78)? 
Рис.78
Рис.78
Решение. На каток действуют активные силы 
, 
Под действием силы 
каток может катиться влево. Вследствие деформации катка возникает момент сопротивления качению, минимальное значение которого равно . Кроме того на каток действуют реакции поверхности – это нормальная реакция и сила трения скольжения , приложенная в точке контакта катка и поверхности.
Так как требуется определить наибольший модуль силы для того чтобы началось качение катка, то предполагается, что он еще находится в покое.
Составим уравнения равновесия сил, действующих на каток.
; 
;
; 
;
; 
.
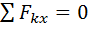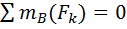Решим составленные уравнения: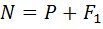 
,
, 
,
Следовательно, при равновесии значение модуля силы равно
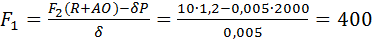Н.
Если значение модуля силы 
будет больше 
Н, то каток начнет катиться.
Ответ: 
Н.
 |
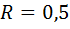м, коэффициент трения качения 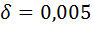м, момент пары сил 
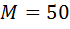Нм. Определить наибольший вес тела 1, при котором оно начинает скользить, если коэффициент трения скольжения для катка и тела 
(рис.79).
Рис.79
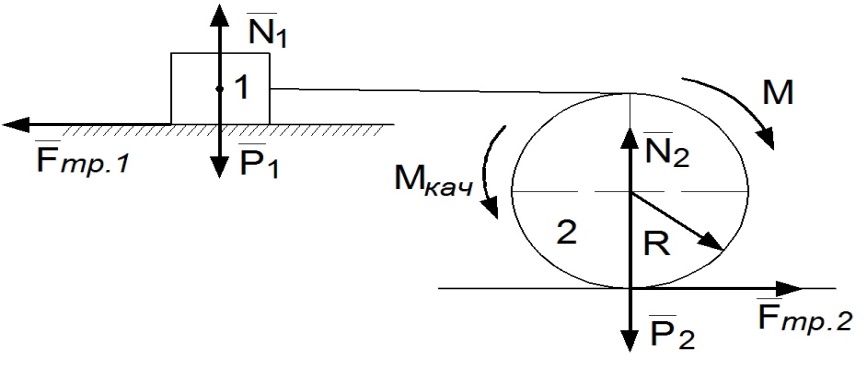
Решение. На груз 1 и каток 2 действуют силы тяжести 
, 
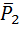, сила трения скольжения между поверхностью и грузом 1 
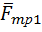, сила трения скольжения между поверхностью и катком 2 
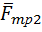, нормальные реакции поверхностей 
, 
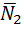. Каток 2 приводится в движение вращающим моментом М = 
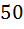Нм. Вследствие деформации катка возникает момент сопротивления качению, минимальное значение которого равно 
. Так как момент сопротивления препятствует качению катка, то его направление противоположно вращающему моменту М.
Силы трения скольжения будут соответственно равны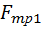 
= 
, 
= 
.
 |
 |
Рис. 80
Так как требуется определить наибольший вес тела 1, при котором начнется его скольжение, то предполагается, что и тело и каток еще находятся в покое. Составим уравнения равновесия для тела 1 и катка 2, отбросив между ними связь - это нить, а ее действие заменим реакцией нити 
.
Уравнения равновесия для тела 1:
1. ; 
= 
;
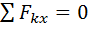2. ; 
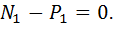
Из второго уравнения 
, а из первого 
= 
Для катка 2 выполняются следующие уравнения равновесия:
1. ; 
= ;
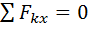2. ; 
;
3. ; 
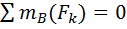Из второго уравнения 
. Третье уравнение преобразуем, подставив в него найденные значения сил:
, 
Ответ: 
Н.
Задача 4. Однородный каток 1 весом 10 кН и радиусом 0,5 м связан грузом 3 горизонтальной нерастяжимой нитью, перекинутой через блок 2. Определить вес груза 3, при котором каток будет оставаться в покое или катиться, если коэффициент трения качения 
м, а коэффициент трения скольжения между катком и поверхностью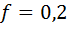 
(рис. 81).
 |
Рис. 81
Решение. На каток действуют силы тяжести , сила трения скольжения , пара сил сопротивления качению с моментом и нормальная реакция плоскости . Каток может катиться под действием груза 3, вес которого равен . Поэтому отбросим мысленно груз 3 и блок 2, а их действие заменим реакцией нити, направленной вдоль нити и численно равной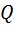 
.
Предположим, что каток находится в покое, тогда выполняются следующие уравнения равновесия:
1. ; ;
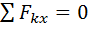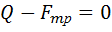2. ; 
;
3. ; 
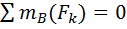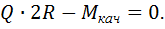
Из второго уравнения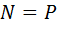 
. Минимальное значение момента сопротивления качению, при котором каток остается в покое, определяется по формуле , и, следовательно, в данной задаче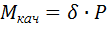 
.
Минимальное значение силы 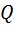, при котором каток остается в покое, определим из третьего уравнения:
. Отсюда 
= 
=0,08 Н. Тогда при значении силы 
0,08 Н каток будет оставаться в покое.
Из первого уравнения определим вес груза 3
= 
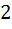Н.
Таким образом, если вес груза 3 будет изменяться в пределах 
Н, то каток будет катиться без скольжения. При дальнейшем увеличении веса груза 3 
Н, каток будет катиться со скольжением.
Как показали расчеты, для начала качения катка требуется значительно меньшая сила, чем для начала его скольжения. С точки зрения энергетических затрат этим объясняется преимущество шариковых и роликовых подшипников по сравнению с подшипниками скольжения.
Ответ: при 0,08 Н каток будет оставаться в покое;
при 
Н каток будет катиться без скольжения;
при Н каток будет катиться со скольжением.
