Отображение области 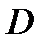 , заданное аналитической функцией
, заданное аналитической функцией 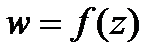 , называется конформным.
, называется конформным.
Отображение, осуществляемое линейной функцией 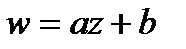 , отображает треугольник
, отображает треугольник 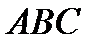 в подобный треугольник
в подобный треугольник 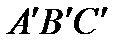 . Координаты точек
. Координаты точек 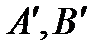 и
и 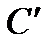 находятся в результате подстановки значений координат точек
находятся в результате подстановки значений координат точек 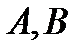 и
и 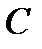 в функцию
в функцию 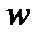 .
.
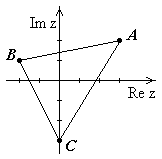 Пример. Найти образ треугольника с вершинами в точках
Пример. Найти образ треугольника с вершинами в точках 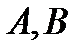 и
и 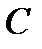 при отображении
при отображении 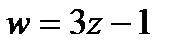 , если
, если 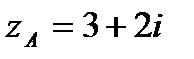 ,
, 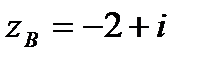 ,
, 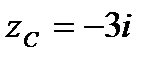 .
.
Решение.
Найдем 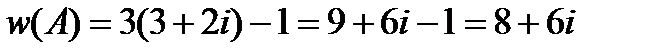 ,
,
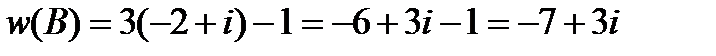 ,
,
| Рис.13 |
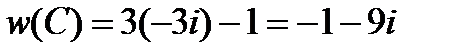 .
.
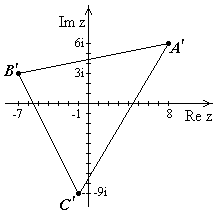 Изобразим на координатной плоскости
Изобразим на координатной плоскости 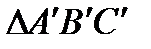 - образ
- образ 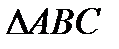 .
.
Дробно-линейная функция 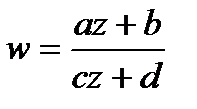 отображает окружность в окружность (прямая линия считается окружностью бесконечного радиуса).
отображает окружность в окружность (прямая линия считается окружностью бесконечного радиуса).
| Рис.14 |
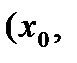
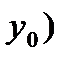 , отображаются в две соответствующие линии, пересекающиеся в точке
, отображаются в две соответствующие линии, пересекающиеся в точке 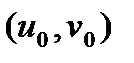 так, что угол
так, что угол 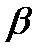 между касательными к исходным и отображенным линиям один и тот же.
между касательными к исходным и отображенным линиям один и тот же.
Задача 11. Заданы уравнения линий, отображающих область 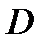 . Найти ее образ при дробно-линейном отображении
. Найти ее образ при дробно-линейном отображении 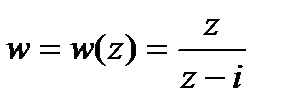 .
.
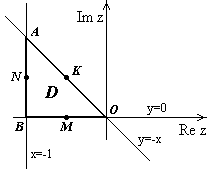 Решение: Построим область
Решение: Построим область 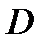 :
: 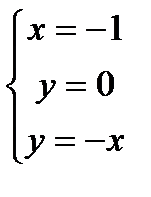 . Из рисунка видно, что
. Из рисунка видно, что 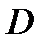 - треугольник
- треугольник 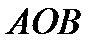 . Найдем
. Найдем
образы точек 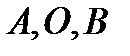 при заданном отображении:
при заданном отображении: 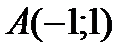
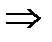
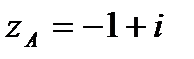 .
.
| Рис.15 |
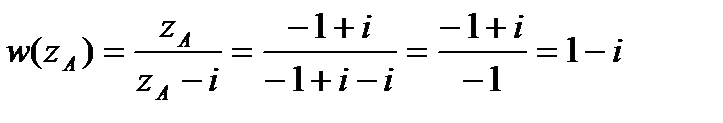
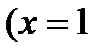 ,
, 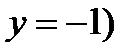
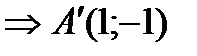 ,
,
| Рис.15 |
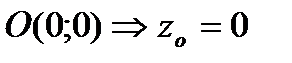
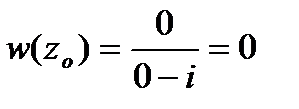
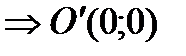 ,
,
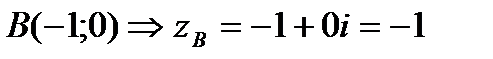 ,
,
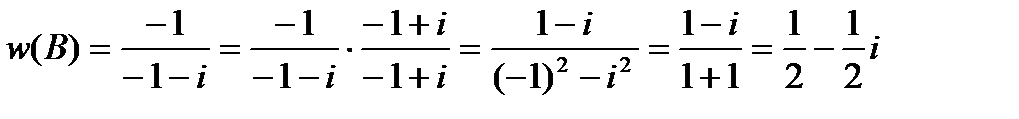 .
.
Т.к. отображение дробно-линейное, то окружность отображается в окружность.
Возьмем дополнительные точки области 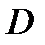 - середины отрезков
- середины отрезков 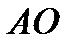 ,
, 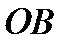 ,
, 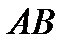 :
: 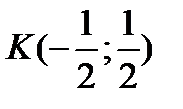 ,
, 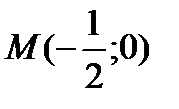 ,
, 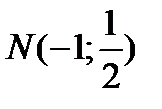 .
.
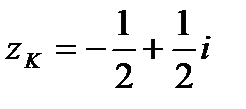 ,
,  ,
, 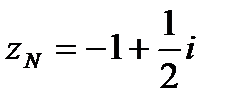 .
.
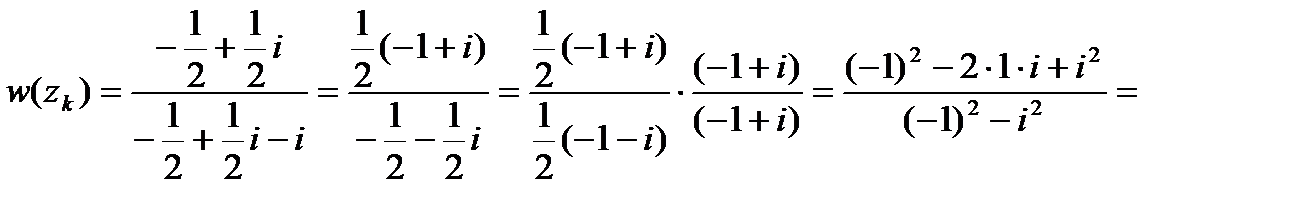
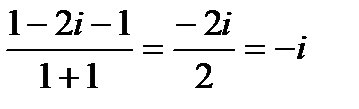
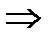
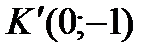 .
.
Отрезок 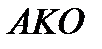 отображается в дугу
отображается в дугу 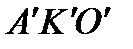 .
.
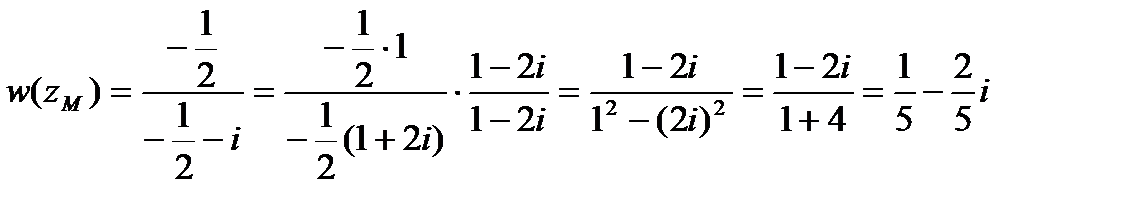 ,
, 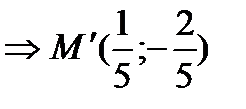 .
.
 Отрезок
Отрезок 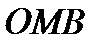 отображается в дугу
отображается в дугу 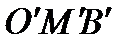 .
.
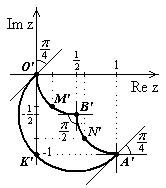
| Рис.16 |
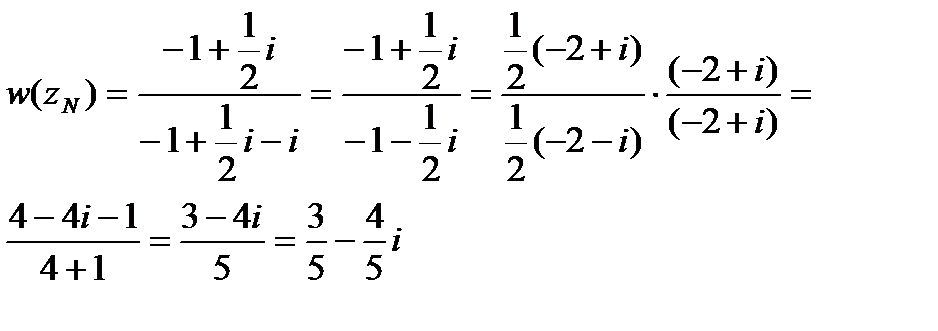
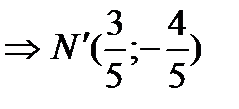 .
.
Проверим свойства сохранения углов:
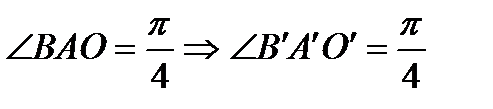 ,
, 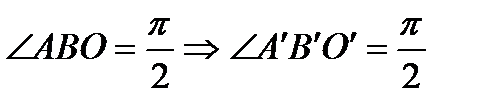 (углы между касательными к дугам
(углы между касательными к дугам 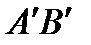 и
и 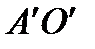 ,
, 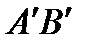 и
и 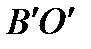 )и т.д.
)и т.д.
Область 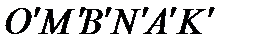 - образ области
- образ области 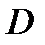 при заданном отображении
при заданном отображении 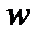 .
.
Замечание: Если в результате отображения 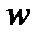 некоторая точка
некоторая точка 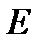 отображается в
отображается в
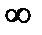 , то считаем, что
, то считаем, что 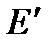 - все точки окружности с радиусом
- все точки окружности с радиусом 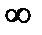 .
.
Пусть 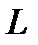 - произвольная гладкая кривая, лежащая в области
- произвольная гладкая кривая, лежащая в области 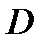 ,
, 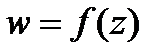 - функция комплексного переменного, непрерывная в области
- функция комплексного переменного, непрерывная в области 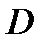 . Тогда по определению
. Тогда по определению
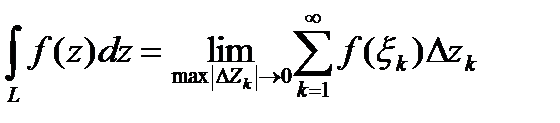 , (
, (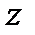 -маленькая) если предел в правой части существует и не зависит ни от способа разбиения дуги
-маленькая) если предел в правой части существует и не зависит ни от способа разбиения дуги 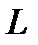 на частичные дуги
на частичные дуги 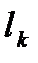 точками
точками 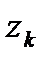 , ни от выбора точек
, ни от выбора точек 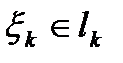 .
.
Если функция 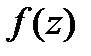 -аналитическая функция в области
-аналитическая функция в области 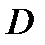 , то значение интеграла
, то значение интеграла 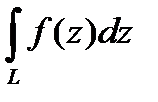 не зависит от линии
не зависит от линии 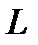 , а зависит от значений начальной и конечной точек этой линии
, а зависит от значений начальной и конечной точек этой линии 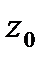 и
и 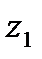 . Тогда
. Тогда 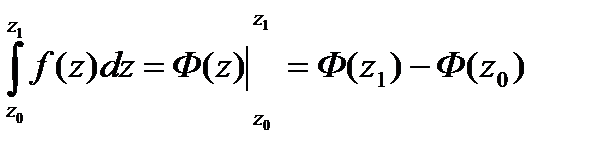 , где
, где 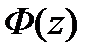 -первообразная функции
-первообразная функции  . Т.е. для вычисления интеграла от аналитической функции
. Т.е. для вычисления интеграла от аналитической функции 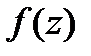 применяют обычные формулы интегрирования и формулу Ньютона-Лейбница.
применяют обычные формулы интегрирования и формулу Ньютона-Лейбница.
Теорема Коши. Если 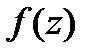 -аналитическая функция в области
-аналитическая функция в области 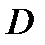 , то интеграл
, то интеграл 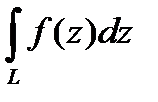 , взятый по любому замкнутому контуру
, взятый по любому замкнутому контуру 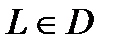 ,
, 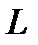 равен нулю.
равен нулю.
Если 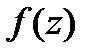 не является аналитической функцией, причем
не является аналитической функцией, причем 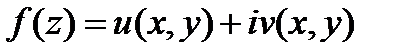 , то вычисление интеграла
, то вычисление интеграла 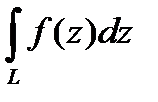 сводится к вычислению двух криволинейных интегралов второго рода:
сводится к вычислению двух криволинейных интегралов второго рода:
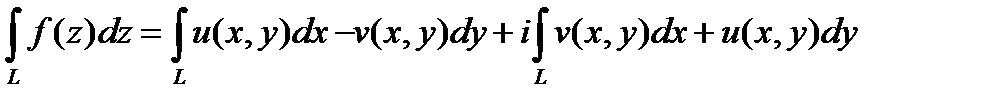 . (29)
. (29)
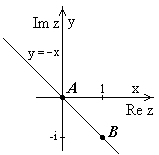 Задача 12.1.
Задача 12.1. 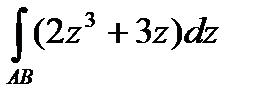 ,
, 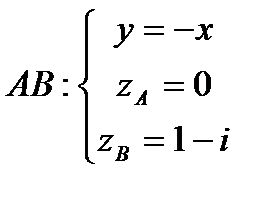 .
.
| Рис.17 |
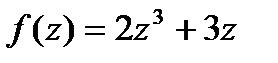 является аналитической. Тогда можно воспользоваться формулой Ньютона-Лейбница, учитывая, что интеграл не зависит от пути интегрирования, а зависит только от начальной и конечной точек.
является аналитической. Тогда можно воспользоваться формулой Ньютона-Лейбница, учитывая, что интеграл не зависит от пути интегрирования, а зависит только от начальной и конечной точек.
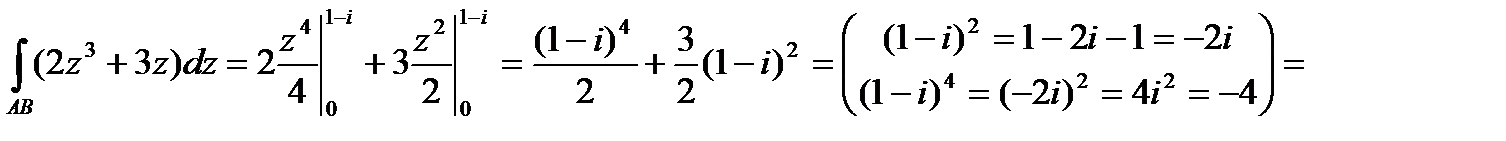
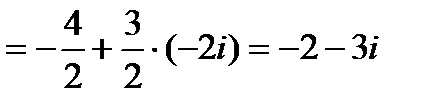 .
.
Задача 12.2. 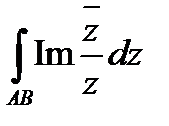 ,
, 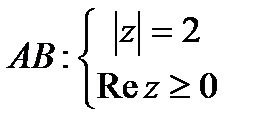 .
.
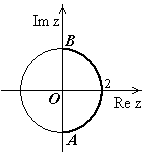 Решение. Функция
Решение. Функция 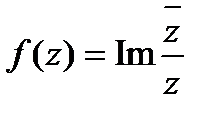 - не является аналитической, значит требуется вычисление при помощи криволинейных интегралов. Путь интегрирования на чертеже:
- не является аналитической, значит требуется вычисление при помощи криволинейных интегралов. Путь интегрирования на чертеже: 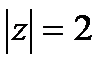 - окружность с центром в т.
- окружность с центром в т.  и радиусом 2;
и радиусом 2; 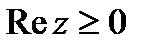 -берем только правую половину окружности.
-берем только правую половину окружности. 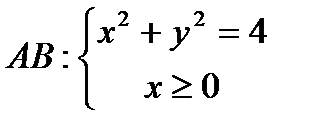 .
.
Найдем действительную и мнимую часть функции 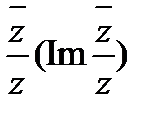 :
:
| Рис.18 |
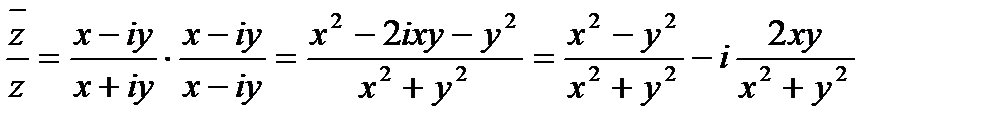 .
.
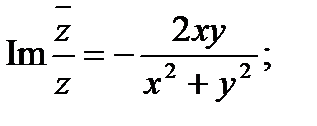
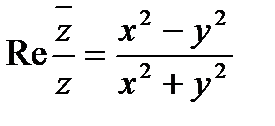 ,
,
т.к. 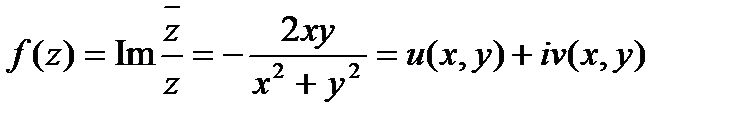 , где
, где 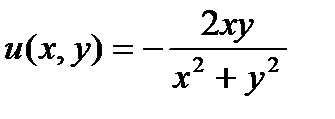 ;
; 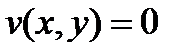 .
.
Тогда 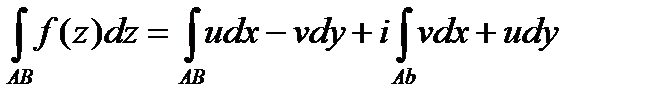 , т.е.
, т.е.
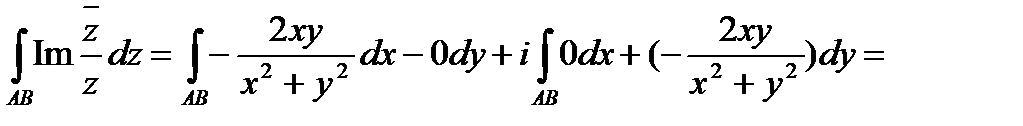
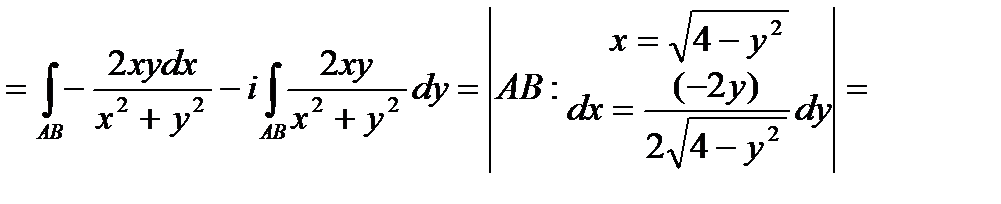
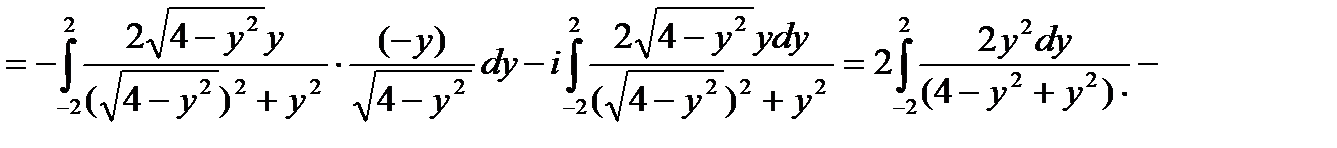
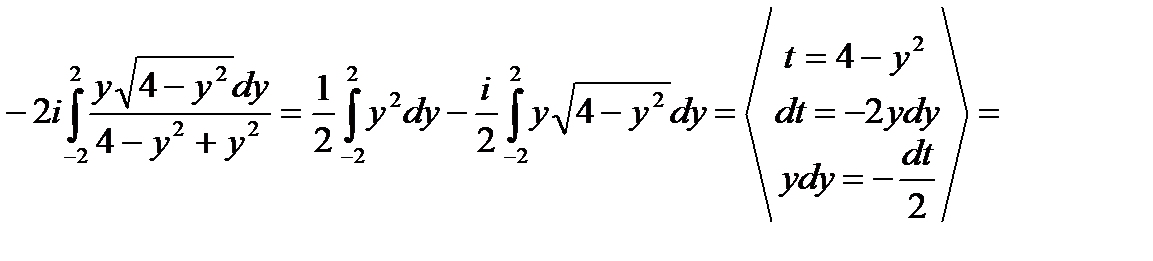
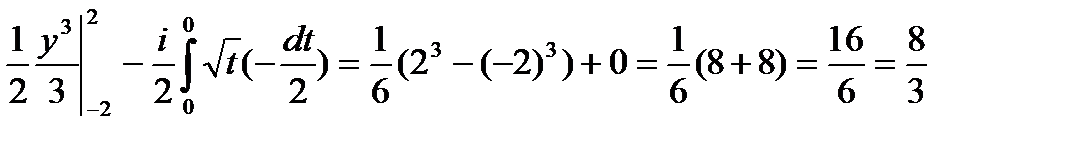
Ряды Лорана
Пусть 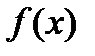 - однозначная и аналитическая функция в кольце
- однозначная и аналитическая функция в кольце 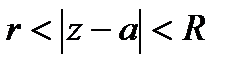 . Эта функция в указанном кольце может быть представлена в виде суммы ряда
. Эта функция в указанном кольце может быть представлена в виде суммы ряда
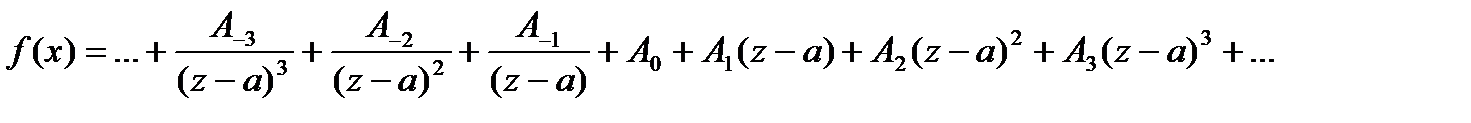 (30)
(30)
Ряд в правой части равенства называется разложением в ряд Лорана функции 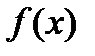 . Коэффициенты этого ряда вычисляются по формуле:
. Коэффициенты этого ряда вычисляются по формуле:
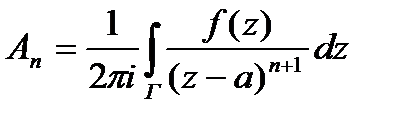 ,
, 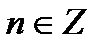 . (31)
. (31)
Заметим, что ряд Лорана состоит их двух частей:
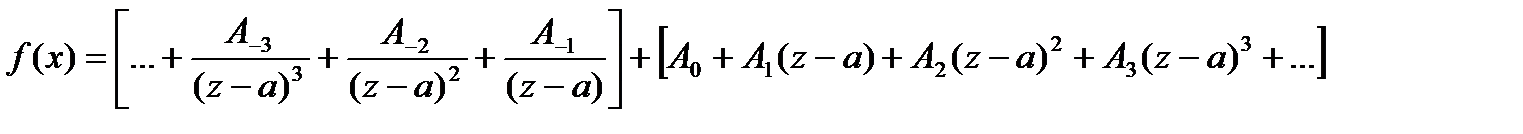
Ряд, стоящий в первой скобке, называется главной частью ряда Лорана, а ряд во второй скобке – правильной частью ряда Лорана.
Вычисление коэффициентов 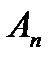 с помощью интегралов (31) часто бывает достаточно сложным. Поэтому для разложения функций в ряды Лорана используют искусственные приемы. Например, для разложения некоторых функций используют разложение в ряд Тейлора, а для разложения рациональных дробей используют сначала разложение на простые дроби, а затем используют формулу суммы бесконечно убывающей геометрической прогрессии (
с помощью интегралов (31) часто бывает достаточно сложным. Поэтому для разложения функций в ряды Лорана используют искусственные приемы. Например, для разложения некоторых функций используют разложение в ряд Тейлора, а для разложения рациональных дробей используют сначала разложение на простые дроби, а затем используют формулу суммы бесконечно убывающей геометрической прогрессии (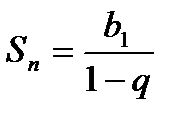 , где
, где 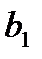 -первый член геометрической прогрессии,
-первый член геометрической прогрессии,  - знаменатель).
- знаменатель).
Задача 13.1. Разложить функцию 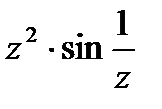 в ряд Лорана в кольце
в ряд Лорана в кольце 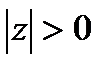 .
.
Решение. Найдем разложение в ряд Тейлора функции 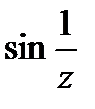 , учитывая, что
, учитывая, что
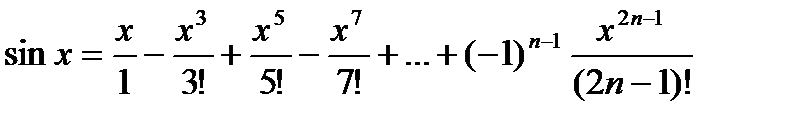 ,
, 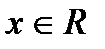 , тогда
, тогда
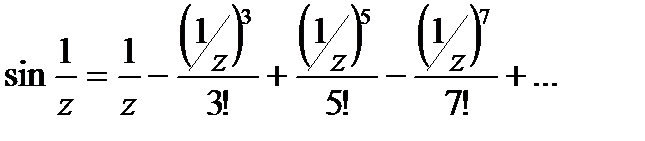
Следовательно: 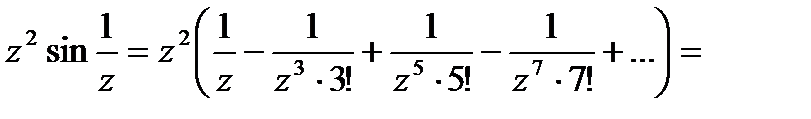
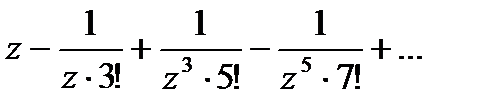 -разложение в ряд Лорана указанной функции.
-разложение в ряд Лорана указанной функции.
Задача 13.2. Разложить функцию 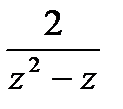 в ряд Лорана в кольце
в ряд Лорана в кольце 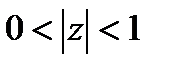 .
.
Решение. Разложим дробь 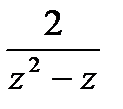 на элементарные дроби:
на элементарные дроби:
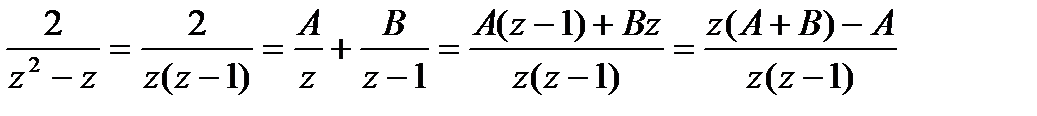
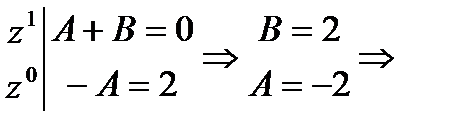
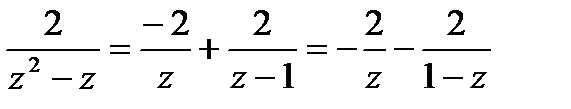 .
.
Т.к. в условии указано кольцо 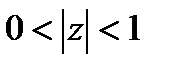 , то разложение нужно искать по степеням
, то разложение нужно искать по степеням 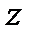 (если указано кольцо
(если указано кольцо 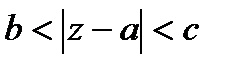 , тогда разложение по степеням
, тогда разложение по степеням 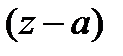 ). В таком случае дробь
). В таком случае дробь 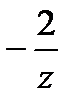 -уже является разложением в ряд Лорана.
-уже является разложением в ряд Лорана.
Дробь 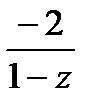 представим как сумму бесконечно убывающей геометрической прогрессии:
представим как сумму бесконечно убывающей геометрической прогрессии: 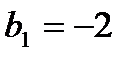 ,
, 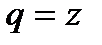 (т.к. из условия задачи
(т.к. из условия задачи 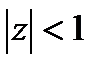 , то что прогрессия с
, то что прогрессия с 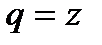 -убывающая):
-убывающая):
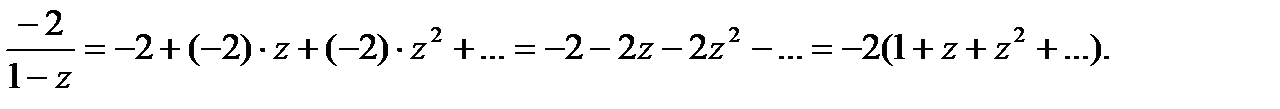
Итого, разложение указанной функции в ряд Лорана имеет вид:
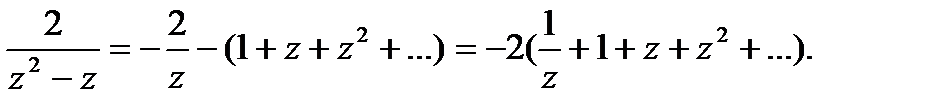
Вычеты функции
Если ряд Лорана содержит главную часть, то 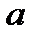 называется изолированной особой точкой. Коэффициент
называется изолированной особой точкой. Коэффициент 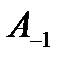 называется вычетом функции
называется вычетом функции 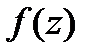 относительно изолированной особой точки
относительно изолированной особой точки 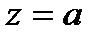 .
.
Изолированная особая точка 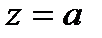 является полюсом
является полюсом 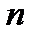 -го порядка, если главная часть содержит конечное число (
-го порядка, если главная часть содержит конечное число (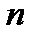 ) членов разложения, т.е. имеет вид:
) членов разложения, т.е. имеет вид:
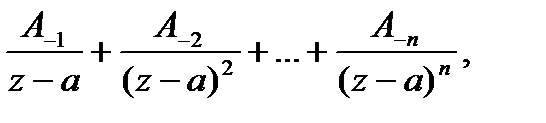
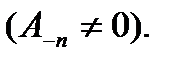
Замечание 1. Пусть 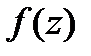 можно представить в виде:
можно представить в виде: 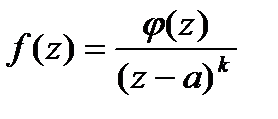 , тогда
, тогда 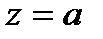 является нулем кратности
является нулем кратности 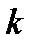 функции
функции 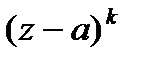 , и
, и 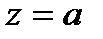 -полюс того же порядка функции
-полюс того же порядка функции 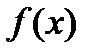 .
.
Замечание 2. Если 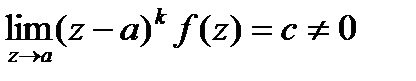 , то
, то 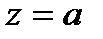 -полюс
-полюс 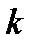 -го порядка функции
-го порядка функции 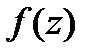 .
.
Пусть 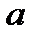 -полюс
-полюс 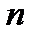 -го порядка функции
-го порядка функции 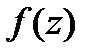 . Вычет функции
. Вычет функции 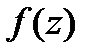 относительно ее полюса
относительно ее полюса 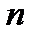 -го порядка вычисляется по формуле:
-го порядка вычисляется по формуле:
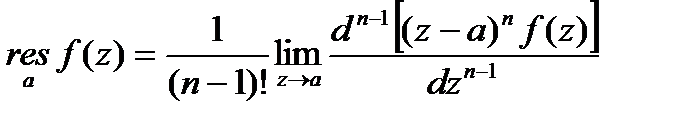 - (residue-вычет), где
- (residue-вычет), где
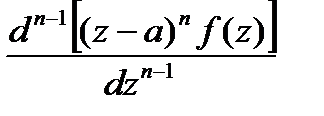 - производная
- производная 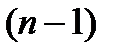 -го порядка от функции
-го порядка от функции 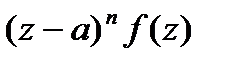 .
.
Задача 14.а). Найти вычеты функции 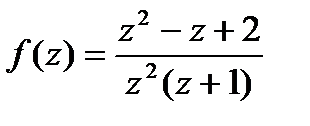 .
.
Решение. Т.к. знаменатель обращается в 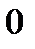 при
при 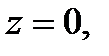
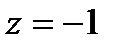
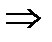
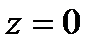 -полюс второго порядка функции
-полюс второго порядка функции 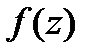 ,
, 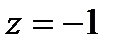 полюс 1-го порядка.
полюс 1-го порядка.
Найдем вычет функции 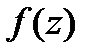 относительно ее полюса второго порядка (
относительно ее полюса второго порядка (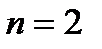 )
) 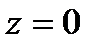 :
:
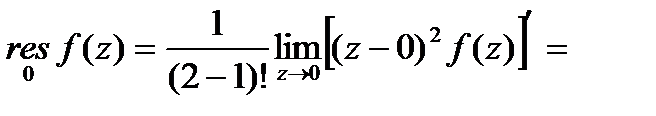 (производная первого порядка, т.к.
(производная первого порядка, т.к. 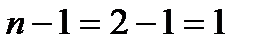 )
)
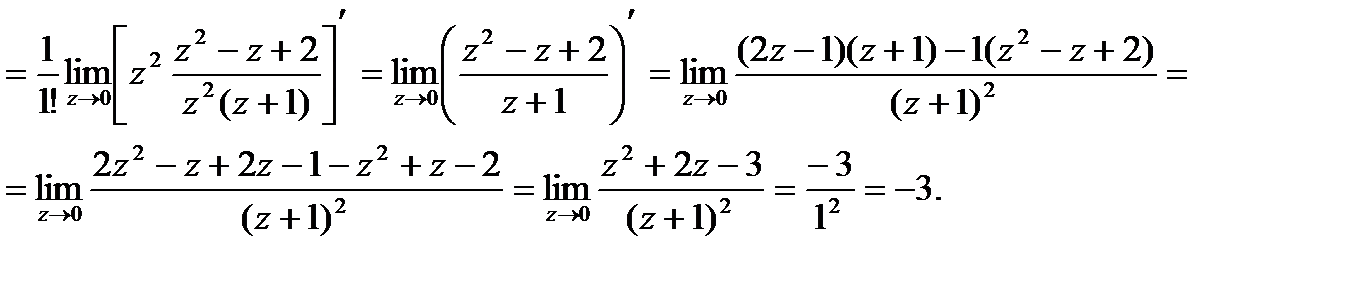
Найдем вычет функции 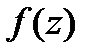 относительно
относительно 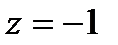 - полюс 1-го порядка
- полюс 1-го порядка
(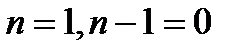 ):
):
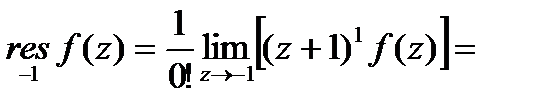 (производная должна быть нулевого порядка, т.е. сама функция)
(производная должна быть нулевого порядка, т.е. сама функция) 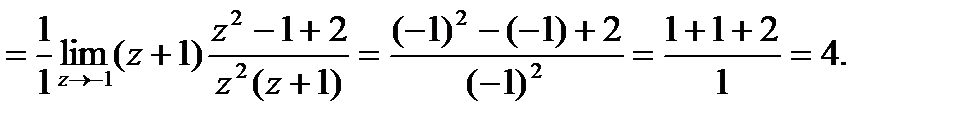
Задача 14.б. Найти вычеты функции 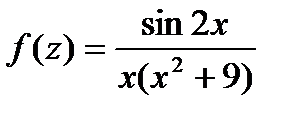 в 0 при
в 0 при 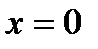 ,
, 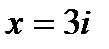 ,
, 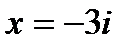 .
.
Решение. Знаменатель обращается в 0.
Но 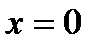 не является полюсом первого порядка, т.к. на основании замечания 2:
не является полюсом первого порядка, т.к. на основании замечания 2:
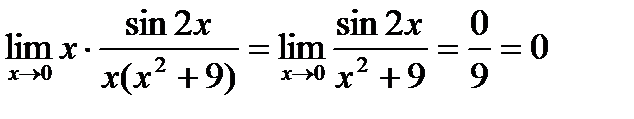 .
.
Итого, полюсы 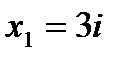 и
и 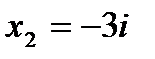 .
.
Найдем вычеты функции 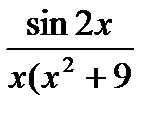 относительно ее полюсов первого порядка (
относительно ее полюсов первого порядка (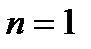 ,
, 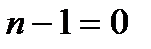 , т.е. используем саму функцию при вычислении предела):
, т.е. используем саму функцию при вычислении предела):
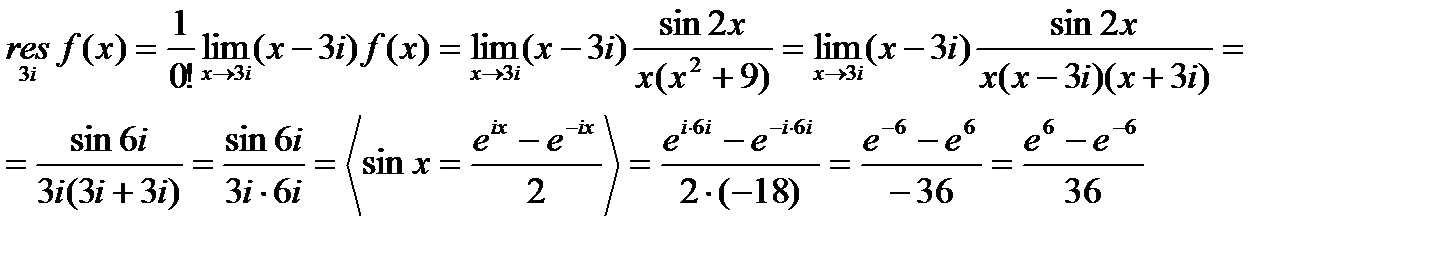 .
.
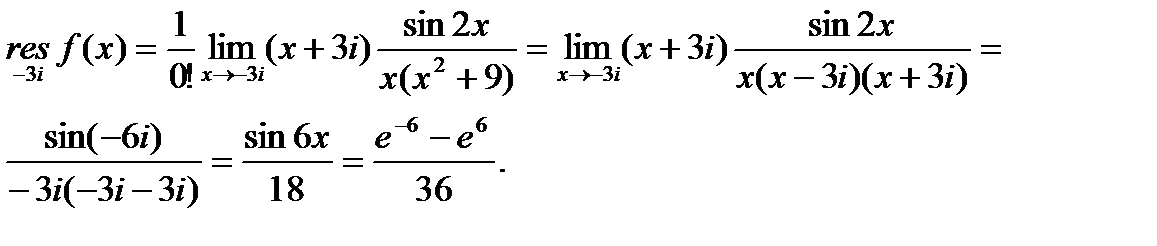
 2018-02-13
2018-02-13 532
532








