Тригонометрическая форма комплексного числа

Рис.5

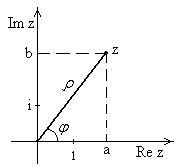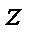Любую точку на плоскости можно задать ее координатами как в декартовой, так и в полярной системе координат. Тогда комплексные числа будут иметь различные формы представления. Пусть - расстояние от точки  до центра координат (точки ),  - угол между радиус-вектором  и действительной осью (рис.5). Из геометрии следует: .

Тогда  или

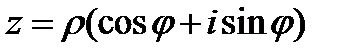 - тригонометрическая форма комплексного числа.                   (5)                                      

 - называют модулем, а  - аргументом комплексного числа и обозначают: , .

По теореме Пифагора ; (6)                                       

.                                                                               (7)

определен с точностью до периода .В качестве главного аргумента принимают значение полярного угла, удовлетворяющее неравенству  или .

 

Тогда ().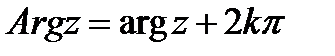

Для не определен, а  равен 0.

Задача 2. Найти модуль и аргумент комплексного числа: а) ,

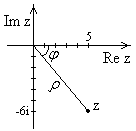б) , в)

Решение: а)

Рис.6

По формуле (7) , тогда , .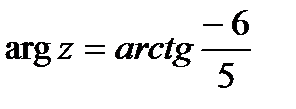

б) , , тогда 

.

По определению функции , где 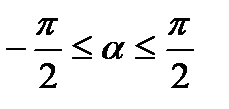. Но для заданного числа

Рис.7

.

Тогда

 

в) , .

.

Рис.8

неопределен, но из геометрического представления заданного числа легко понять, что , .

 

 Неравенство , где 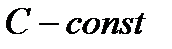, задает множество точек , лежащих на окружности с центром  и радиусом , т.к. - расстояние от точки  до точки .

Задача 3. Найти и изобразить на плоскости множество значений комплексных чисел, удовлетворяющих неравенству: , .

Решение. Преобразуем неравенство . Требуется найти множество комплексных чисел таких, что расстояние от каждой из них до числа  было меньше 2. Нарисуем окружность с центром в точке  и радиусом 2. Ясно, что искомые точки лежат внутри окружности. Учитывая значения , искомые точки принадлежат заштрихованной области (рис 9).

Рис.9

Произведение комплексных чисел, заданных в тригонометрической форме

Пусть дано два комплексных числа, заданных в тригонометрической форме: , 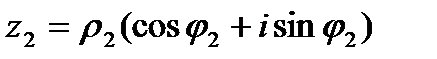. Тогда

, т.е.                                                                               (8)

; .

Задача 4. Найти произведение чисел 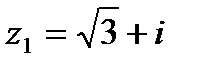 и .

Решение.

, , .

, , .

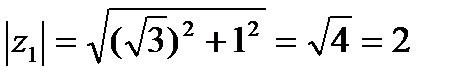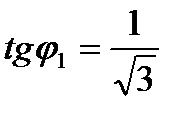Рис.10

Тогда

.

Формула Эйлера

Воспользуемся разложением в ряд Тейлора-Маклорена функций:

В последнюю формулу вместо  подставим :

                                                                                  (9)

Тогда 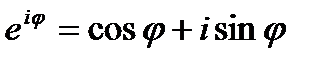 - формула Эйлера.

Подставив в формулу , получим соотношение между числами: .

А именно ,

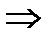
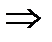
Используя формулу Эйлера, была получена показательная форма комплексного числа:

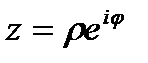(10)

Тогда: (11)

Последнее равенство подтверждает правило для вычисления произведения комплексных чисел: модули перемножаются, аргументы суммируются.

Используя формулу произведения комплексных чисел в а) показательной и б) тригонометрической формах, легко получить форму возведения в степень:

а)  ,

б) - формула Муавра                                                   (12)

Аналогично .                                      (13)           

Следует заметить, что для нахождения угла  требуется учитывать не только полярный угол , но и период , т.е. .                                 (14)

Задача 5.1. Найти значение выражения , для ; а) ; б) .

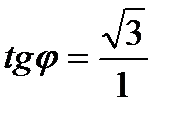
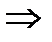
Решение. По формуле (6) . Воспользовавшись формулой (7), получим: . Запишем заданное число в показательной форме: .

Найдем .

а) .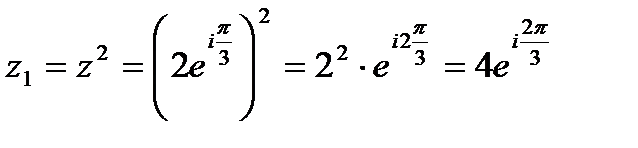

Рис.11

б) .

Тогда, если : ;

: ;

:  - графическое изображение совпадает с , все следующие углы будут повторять уже найденные.

Итого, .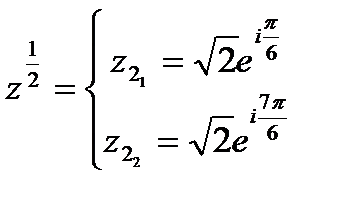

Задача 5.2. Найти .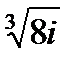

Решение. 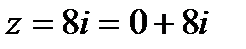. По формулам (6) и (7) получим:

, , .

.

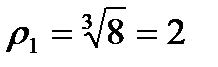По формуле (14) получим: .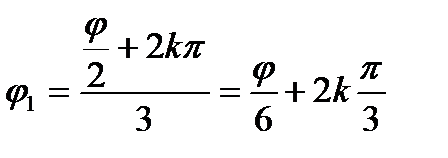

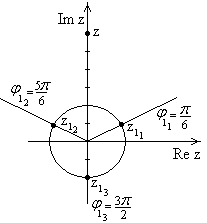
Тогда:

: ;

: ;

Рис.12

: ;

:  - графическое изображение совпадает с . Т.к. для всех корней () они лежат на окружности радиуса 2.

Найдем алгебраическую форму этих корней:

;

;

.