Задача №1
Даны координаты вершин треугольника  :
: 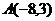 ,
, 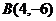 ,
, 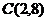 . Найти:
. Найти:
1) уравнения сторон  и
и  и их угловые
и их угловые
коэффициенты;
2) угол  в радианах (градусах) с точностью до двух знаков после запятой;
в радианах (градусах) с точностью до двух знаков после запятой;
3) уравнение высоты  и ее длину;
и ее длину;
4) уравнение медианы  и координаты точки
и координаты точки  пересечения этой медианы с высотой
пересечения этой медианы с высотой  .
.
 Сделать чертеж (рис.1).
Сделать чертеж (рис.1).
Рис. 1
Решение. 1) Найдем координаты векторов 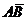 и
и 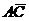 , для чего воспользуемся формулой
, для чего воспользуемся формулой
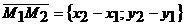 .
.
Тогда 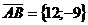 ,
, 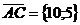 . Эти векторы являются направляющими векторами прямых, на которых лежат соответствующие стороны треугольника и для получения их уравнений можно использовать каноническое уравнение прямой на плоскости
. Эти векторы являются направляющими векторами прямых, на которых лежат соответствующие стороны треугольника и для получения их уравнений можно использовать каноническое уравнение прямой на плоскости
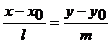 .
.
В результате получим
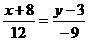 (
( ),
),
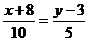 (
( ).
).
Разрешая эти уравнения относительно 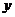 , т.е. приводя их к виду уравнения прямой с угловым коэффициентом
, т.е. приводя их к виду уравнения прямой с угловым коэффициентом
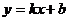 ,
,
найдем 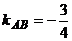 ,
, 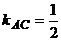 .
.
2) Угол  треугольника совпадает с углом между векторами
треугольника совпадает с углом между векторами 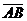 и
и 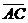 и для его нахождения можно использовать формулу
и для его нахождения можно использовать формулу
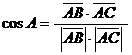 ,
,
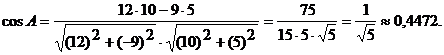 По таблице найдем значение угла
По таблице найдем значение угла  : <
: < 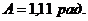 (
(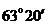 ).
).
3) Для получения уравнения высоты  приведем уравнение стороны
приведем уравнение стороны  к виду общего уравнения прямой на плоскости
к виду общего уравнения прямой на плоскости
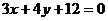 (
( ).
).
Из рисунка видно, что вектор нормали к прямой  является направляющим вектором высоты
является направляющим вектором высоты  , т.е.
, т.е. 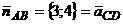 , и можно вновь воспользоваться каноническим уравнением прямой на плоскости
, и можно вновь воспользоваться каноническим уравнением прямой на плоскости
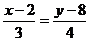 (
( ).
).
Длину высоты  вычислим по формуле вычисления расстояния от точки
вычислим по формуле вычисления расстояния от точки 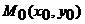 до прямой
до прямой 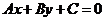 :
:
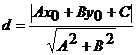 .
.
В нашем случае 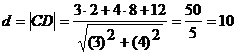 .
.
4) Найдем координаты точки 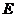 , являющейся серединой отрезка
, являющейся серединой отрезка 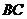
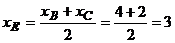 ;
; 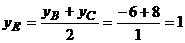 .
.
Т.о., 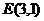 , и для нахождения уравнения медианы
, и для нахождения уравнения медианы  можно использовать уравнение прямой, проходящей через две точки
можно использовать уравнение прямой, проходящей через две точки 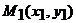 и
и 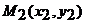 :
: 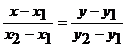 . Тогда получим
. Тогда получим
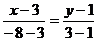 или
или 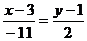 (
( ).
).
Наконец, для вычисления координат точки  , решим совместно уравнения прямых
, решим совместно уравнения прямых  и
и  , предварительно приведя их уравнения к общему виду
, предварительно приведя их уравнения к общему виду
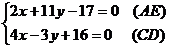 .
.
Отсюда получим 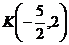 .
.
Задача №2
Даны координаты вершин пирамиды  :
:
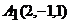 ,
, 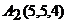 ,
, 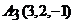 ,
, 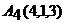 . Найти:
. Найти:
1) длину ребра 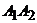 ;
;
2) угол между ребрами  и
и  ;
;
3) уравнение плоскости  и угол между ребром
и угол между ребром
 и плоскостью
и плоскостью  ;
;
4) уравнение высоты, опущенной из вершины 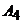 на грань
на грань
 и ее длину;
и ее длину;
5) площадь грани  и объем пирамиды.
и объем пирамиды.
Сделать чертеж.
Решение. 1) Длина ребра  совпадает с расстоянием между точками
совпадает с расстоянием между точками  и
и  :
:
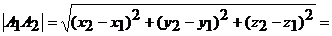
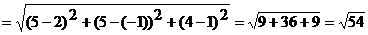 .
.
2) Найдем координаты векторов, которые совпадают с выходящими из вершины 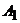 ребрами пирамиды:
ребрами пирамиды:
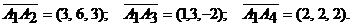
Угол между ребрами  и
и  совпадает с углом между векторами
совпадает с углом между векторами  и
и  . Определим этот угол, используя формулу скалярного произведения векторов:
. Определим этот угол, используя формулу скалярного произведения векторов:
 .
.
Отсюда
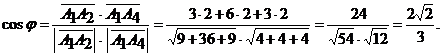 Тогда
Тогда
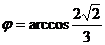 .
.
3) Уравнение плоскости, проходящей через три заданные точки, имеет вид
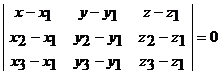 .
.
Подставляя в уравнение координаты точек  ,
,  и
и  получим
получим
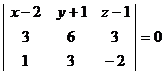 ,
,
или
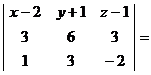
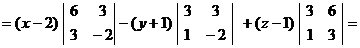
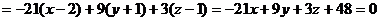 .
.
Таким образом, уравнение плоскости  имеет вид
имеет вид
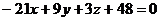 .
.
Составим уравнение прямой, проходящей через точки  и
и  . Уравнение прямой, проходящей через две точки, имеет вид
. Уравнение прямой, проходящей через две точки, имеет вид
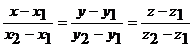 ,
,
где 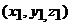 – координаты первой точки,
– координаты первой точки, 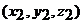 – координаты второй точки. Подставляя в уравнение координаты точек
– координаты второй точки. Подставляя в уравнение координаты точек 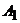 и
и 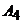 , получим
, получим
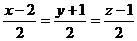 .
.
Угол между прямой 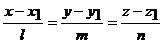 и плоскостью
и плоскостью 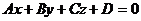 определяется по формуле
определяется по формуле
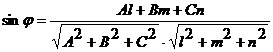
Воспользуемся этой формулой для вычисления угла между ребром 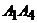 и плоскостью
и плоскостью 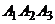 :
:
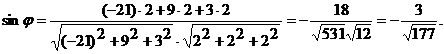
Отсюда 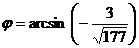 .
.
4) Уравнение высоты найдем как уравнение прямой, проходящей через точку 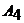 перпендикулярно плоскости
перпендикулярно плоскости  , задаваемой уравнением
, задаваемой уравнением 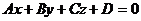 . Из условия перпендикулярности прямой и плоскости следует
. Из условия перпендикулярности прямой и плоскости следует 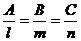 , поэтому уравнение высоты
, поэтому уравнение высоты 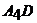 имеет вид
имеет вид
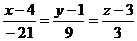 .
.
Для нахождения длины высоты можно использовать формулу 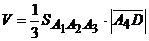 . Объем
. Объем 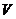 и площадь
и площадь 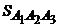 будут найдены в п.5). Поэтому
будут найдены в п.5). Поэтому 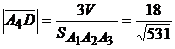 .
.
5) Грань  представляет собой треугольник, площадь которого равна половине площади параллелограмма, построенного на векторах
представляет собой треугольник, площадь которого равна половине площади параллелограмма, построенного на векторах 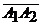 и
и 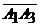 .
.
Найдем векторное произведение этих векторов. Имеем
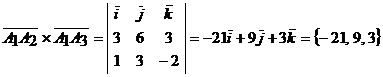 .
.
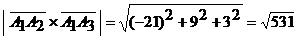 .
.
Следовательно,
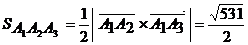 .
.
Для вычисления объема пирамиды воспользуемся смешанным произведением векторов. Напомним, смешанное произведение трех векторов по модулю равно объему параллелепипеда, построенного на этих векторах. А объем пирамиды равен 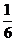 части объема этого параллелепипеда. Имеем
части объема этого параллелепипеда. Имеем
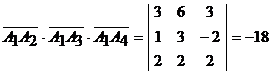 .
.
Поэтому 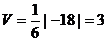 .
.
Задача №3
Найти уравнение геометрического места точек, одинаково удаленных от начала координат и точки 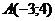 .
.
Решение. Пусть точка  принадлежит искомой прямой. Расстояние между точками
принадлежит искомой прямой. Расстояние между точками 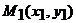 и
и 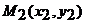 вычисляется по формуле
вычисляется по формуле
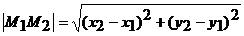 .
.
По условию задачи 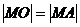 , поэтому
, поэтому 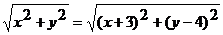 . Возведем обе части уравнения в квадрат. Приводя подобные члены, получим
. Возведем обе части уравнения в квадрат. Приводя подобные члены, получим 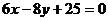 . Это и есть уравнение искомого геометрического места точек. Рекомендуется проверить, что эта прямая перпендикулярна отрезку
. Это и есть уравнение искомого геометрического места точек. Рекомендуется проверить, что эта прямая перпендикулярна отрезку 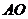 и проходит через его середину.
и проходит через его середину.
Задача №4
Решить систему линейных уравнений методом Гаусса.
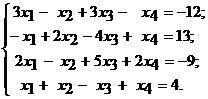
Решение. Метод Гаусса основан на приведении системы уравнений к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы.
Расширенная матрица системы уравнений имеет вид
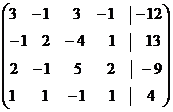
Поменяем местами первую и четвертую строки этой матрицы
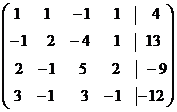 .
.
Сложим первую и вторую строки матрицы. Затем последовательно умножим первую строку на (-2) и на (-3) и сложим с третьей и четвертой строками. Получаем:
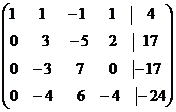 .
.
Сложим вторую и третью строки матрицы. Затем умножим вторую строку на 4, а четвертую на 3 и сложим эти строки. Получим матрицу вида
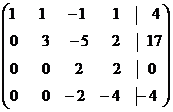 .
.
Сложим третью строку матрицы с четвертой. В результате получим матрицу
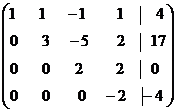 .
.
Полученной матрице соответствует система уравнений вида
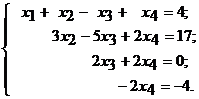
Из последнего уравнения находим 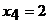 . Из третьего уравнения находим, что
. Из третьего уравнения находим, что 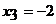 . Из второго уравнения следует, что
. Из второго уравнения следует, что 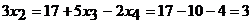 . Откуда
. Откуда 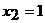 . Подставив найденные значения
. Подставив найденные значения 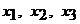 в первое уравнение, получим
в первое уравнение, получим 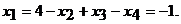
Решение системы: 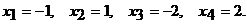
Задача №5
Решить систему линейных уравнений
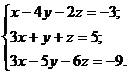
1) методом Крамера;
2) используя обратную матрицу.
Решение. 1) Решим систему уравнений методом Крамера. Решение системы трех линейных уравнений с тремя неизвестными
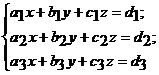
находится по формулам
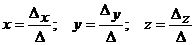 ,
,
где
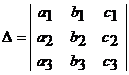 (предполагается, что Δ ≠ 0),
(предполагается, что Δ ≠ 0),
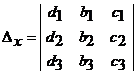 ,
, 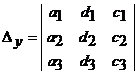 ,
, 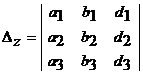 .
.
Для данной системы уравнений имеем
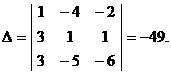
Вспомогательные определители
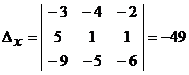 ,
, 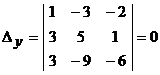 ,
,
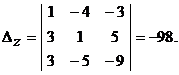
Решение системы уравнений
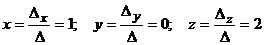 .
.
2) Решим теперь систему матричным методом. Запишем исходную систему уравнений в матричном виде
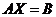 ,
,
где
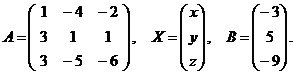
Решение матричного уравнения имеет вид
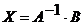 ,
,
где 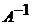 – матрица, обратная к матрице А. Заметим, что поскольку определитель матрицы А не равен нулю (
– матрица, обратная к матрице А. Заметим, что поскольку определитель матрицы А не равен нулю (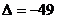 , см. п. 1), то матрица системы невырожденная и, следовательно, имеет обратную.
, см. п. 1), то матрица системы невырожденная и, следовательно, имеет обратную.
Обратная матрица находится по формуле
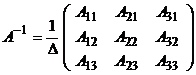 ,
,
где Δ – определитель матрицы А, 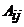 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 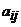 определителя матрицы А. Вычислим алгебраические дополнения:
определителя матрицы А. Вычислим алгебраические дополнения:
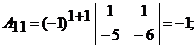
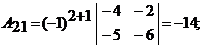
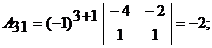
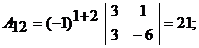
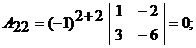
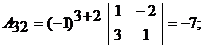
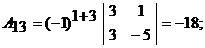
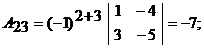
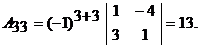
Таким образом,
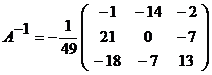 ,
,
откуда
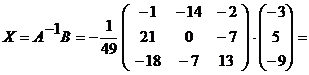
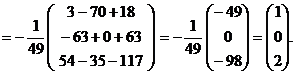
Следовательно, 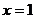 ,
, 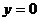 ,
, 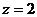 .
.
Задача №6
Вычислить пределы, не пользуясь правилом Лопиталя:
а) 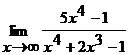 ; б)
; б) 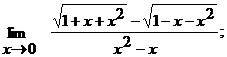
в) 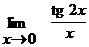 ; г)
; г) 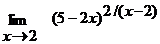 .
.
Решение. а) 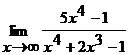 .
.
И числитель, и знаменатель дроби при 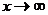 стремятся к бесконечности, т.е. имеем неопределенность вида
стремятся к бесконечности, т.е. имеем неопределенность вида 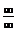 . Разделив числитель и знаменатель на
. Разделив числитель и знаменатель на 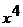 , получим
, получим
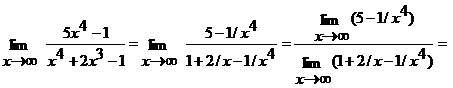
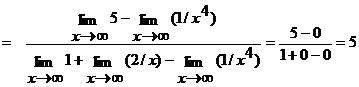 .
.
б) 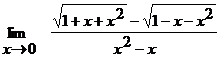 ;
;
И числитель, и знаменатель дроби при 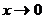 стремятся к нулю. Имеем неопределенность вида
стремятся к нулю. Имеем неопределенность вида 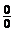 . Умножим числитель и знаменатель на выражение
. Умножим числитель и знаменатель на выражение 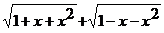 . Получим
. Получим
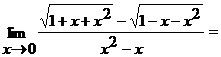
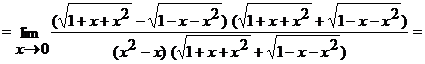
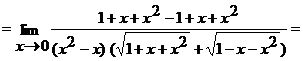
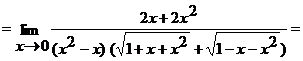
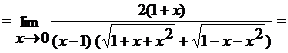
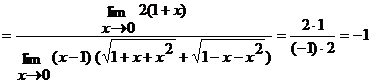 .
.
в) 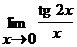 ;
;
Имеем неопределенность вида 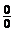 . Воспользуемся первым замечательным пределом
. Воспользуемся первым замечательным пределом 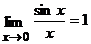 . Получим
. Получим
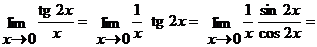
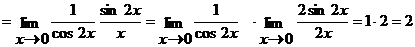 .
.
г) 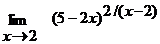 ;
;
Имеем неопределенность вида 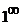 . Воспользуемся вторым замечательным пределом
. Воспользуемся вторым замечательным пределом 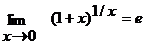 .
.
Введем в рассмотрение новую переменную 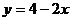 ,
, 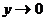 при
при 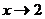 . Тогда
. Тогда 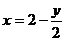 . Переходя к новой переменной, получим
. Переходя к новой переменной, получим
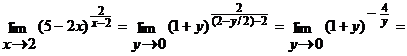
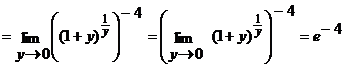 .
.
Задача №7
Исследовать функцию  на непрерывность. Определить характер точек разрыва, если они существуют. Сделать чертеж.
на непрерывность. Определить характер точек разрыва, если они существуют. Сделать чертеж.
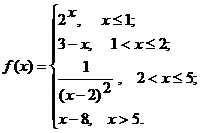
Решение. На промежутке  функция
функция  совпадает с функцией
совпадает с функцией 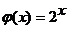 . Это элементарная функция. Указанный промежуток входит в область определения функции
. Это элементарная функция. Указанный промежуток входит в область определения функции  . Значит на промежутке
. Значит на промежутке 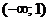 функция
функция 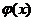 непрерывна, а, следовательно, на этом промежутке непрерывна и функция
непрерывна, а, следовательно, на этом промежутке непрерывна и функция  . Аналогично устанавливается непрерывность функции
. Аналогично устанавливается непрерывность функции  на промежутках (1; 2), (2; 5) и (5; + ∞).
на промежутках (1; 2), (2; 5) и (5; + ∞).
Исследуем функцию  на непрерывность в точках
на непрерывность в точках 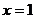 ,
, 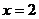 и
и 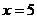 . Функция определена в этих точках:
. Функция определена в этих точках: 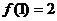 ,
, 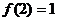 ,
, 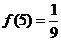 . Вычислим односторонние пределы в этих точках.
. Вычислим односторонние пределы в этих точках.
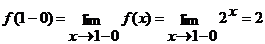 ,
,
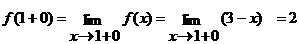 .
.
Таким образом, 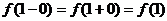 . Следовательно, в точке
. Следовательно, в точке 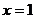 функция
функция  непрерывна.
непрерывна.
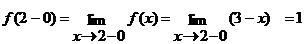 ,
,
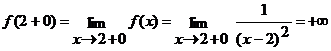 .
.
Так как один из односторонних пределов равен + ∞, то точка 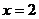 является точкой разрыва второго рода.
является точкой разрыва второго рода.
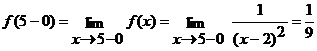 ,
,
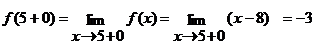 .
.
В точке 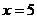 односторонние пределы конечны, но не равны между собой. Следовательно, точка
односторонние пределы конечны, но не равны между собой. Следовательно, точка 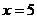 является точкой разрыва первого рода.
является точкой разрыва первого рода.
Сделаем чертеж заданной функции  (рис.2).
(рис.2).
|
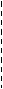







Рис. 2
Задача №8
Найти производные заданных функций.
а) 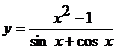 ; б)
; б) 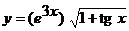 ;
;
в)  ; г)
; г) 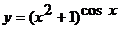 ; д)
; д) 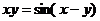 ; е)
; е) 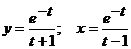 ;
;
Решение. а) 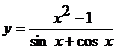 .
.
Применяя правило дифференцирования частного двух функций, получим
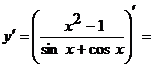
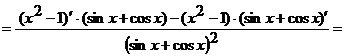
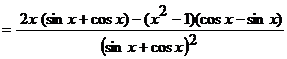 .
.
б) 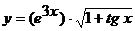 ;
;
Применяя правило дифференцирования произведения двух функций, получим:
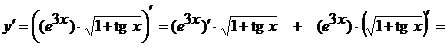
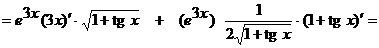
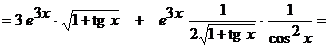
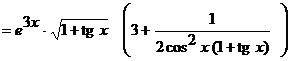 .
.
в) 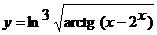 ;
;
Применяя правило дифференцирования сложной функции, получим
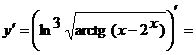
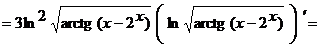
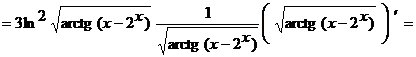
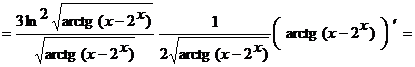
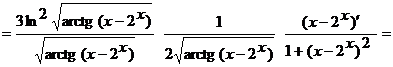
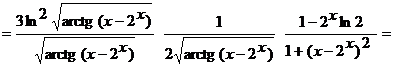
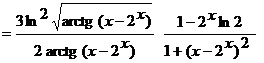 .
.
г) 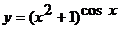 ;
;
И основание, и показатель степени здесь зависят от x. Прологарифмируем равенство:
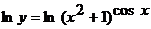 или
или 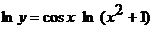 .
.
Продифференцируем обе части последнего равенства по x, учитывая, что 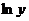 есть сложная функция, так как y является функцией переменной x.
есть сложная функция, так как y является функцией переменной x.
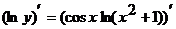 ;
;
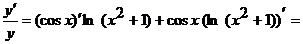
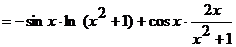 .
.
Следовательно,
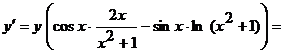
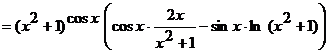 .
.
д) 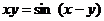 ;
;
Напомним: если функция 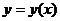 задана неявно соотношением
задана неявно соотношением 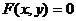 , то производную
, то производную 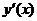 функции
функции 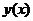 можно найти из уравнения
можно найти из уравнения
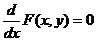 .
.
Перепишем выражение следующим образом:
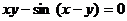 .
.
Продифференцируем по x, учитывая, что y есть функция переменной x
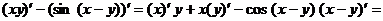
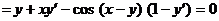 .
.
Выразим 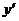
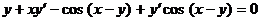 ,
,
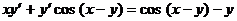 ,
,
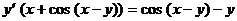 .
.
Таким образом,
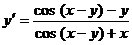 .
.
е) 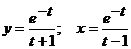 .
.
Функции 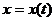 и
и 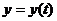 параметрически задают функцию
параметрически задают функцию 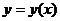 . Ее производная вычисляется по следующей формуле
. Ее производная вычисляется по следующей формуле
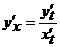 ,
,
где
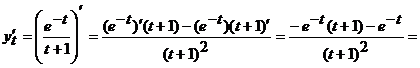
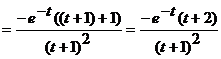 ;
;
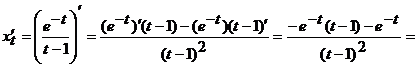
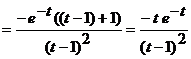 .
.
Отсюда
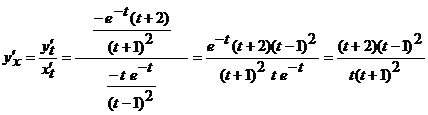 .
.
 2018-02-12
2018-02-12 268
268

 -3
-3