Правая часть данного неоднородного уравнения имеет вид

                ,

в данном случае .  Так как число

 a +bi = i не является корнем характеристического уравнения, то частное решение будем искать в форме

Подставим выражения  и производных в заданное уравнение, получим после приведения подобных членов

Приравняем коэффициенты при  и , получим два уравнения для определения  А и В:

Откуда  Следовательно, частным решением будет . Общее решение будет иметь вид

           .

    Найдем С ₁, С ₂, используя начальные условия,

или  

Отсюда С₁=1, С₂=0. В итоге получаем, что .

     Система дифференциальных уравнений вида

где , , 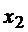…,   – неизвестные функции независимой переменной , называется нормальной системой.

   Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно , , 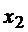…, , то система дифференциальных уравнений называется линейной.

   Иногда, нормальную систему дифференциальных уравнений удается свести к одному уравнению n -го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного (так называемый метод исключения).

   Рассмотрим этот метод на конкретных примерах.

  Пример 13. Найти общее решение системы дифференциальных уравнений

       Решение. Продифференцируем по 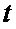 первое уравнение: . Подставляя сюда выражения  и 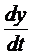 из системы, получим

или имеем . Характеристическое уравнение  имеет корни . Следовательно, общее решение для 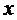 запишется в виде

Общее решение y находим из первого уравнения:

.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ