Для решения задач 1–2 необходимо изучить пункты 1,2 программы.
Пример 1. Найти общее решение дифференциального уравнения 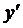 = tg x tg y.
= tg x tg y.
Решение. Полагая  =
= 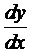 , получим
, получим 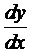 = tg x tg y. Разделяя переменные, приходим к уравнению сtg у dy = tg x dx. Интегрируем:
= tg x tg y. Разделяя переменные, приходим к уравнению сtg у dy = tg x dx. Интегрируем:
 сtg у dy=
сtg у dy=  tg x dx, или ln
tg x dx, или ln  = – ln
= – ln  +ln c.
+ln c.
(Постоянная интегрирования обозначена ln c). Отсюда находим sin y =c/ cos x или sin y cos x =c – общее решение уравнения.
Пример 2. Найти общее решение дифференциального уравнения с разделяющимися переменными.
(1+  ) dy +ydx= 0.
) dy +ydx= 0.
Решение. Преобразуем уравнение к виду  = –
= –  . Интегрируя получим
. Интегрируя получим 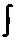
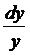 = –
= –  , или ln
, или ln  =
=
= – arctg x + c. Общее решение можно записать в виде 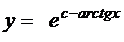 .
.
Пример 3. Найти общее решение однородного дифференциаль-ного уравнения х  = х + 2 у.
= х + 2 у.
Решение. Однородное дифференциальное уравнение первого порядка можно привести к виду  = f (
= f ( ). Чтобы решить уравнение проводят замену
). Чтобы решить уравнение проводят замену  , где u (x) – новая неизвестная функция, после чего уравнение преобразуется в уравнение с разделяющимися переменными.
, где u (x) – новая неизвестная функция, после чего уравнение преобразуется в уравнение с разделяющимися переменными.
Преобразуя исходное уравнение, получим 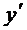 =
=  или
или  =
=  – однородное уравнение. Полагаем
– однородное уравнение. Полагаем  , тогда
, тогда  = u + x
= u + x  . Уравнение запишется x
. Уравнение запишется x  + u = 1 + 2 u или
+ u = 1 + 2 u или  х = 1+ u. Решаем полученное уравнение с разделяющимися переменными
х = 1+ u. Решаем полученное уравнение с разделяющимися переменными
 =1 + u или
=1 + u или  =
=  , интегрируем
, интегрируем 
 =
= 
 , получим ln
, получим ln 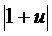 = ln
= ln  + ln
+ ln  . Откуда 1+ u =cx или u= cx – 1. Возвращаясь к старой переменной у по формуле u=
. Откуда 1+ u =cx или u= cx – 1. Возвращаясь к старой переменной у по формуле u=  , получим обще решение
, получим обще решение  .
.
Пример 4. Найти частное решение линейного дифференциаль-ного уравнения первого порядка, удовлетворяющее начальному условию:
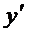 −
− 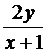 =
=  ,
,  (0) = 1.
(0) = 1.
Решение. Решение уравнения ищем в виде произведения двух функций y = u (x) v (x), вычисляя производную, получим
 =
=  .
.
После подстановки в уравнение, запишем
 =
=  или
или
 =
=  .
.
Выберем функцию v (x) такой, чтобы выполнялось условие  =0. Разделяя переменные в этом уравнении, находим
=0. Разделяя переменные в этом уравнении, находим  или
или  . После интегрирования обеих частей равенства, получим ln
. После интегрирования обеих частей равенства, получим ln  = 2 ln
= 2 ln  + с, т.к. достаточно найти хотя бы одно решение отличное от нуля, то положим с = 0. Тогда
+ с, т.к. достаточно найти хотя бы одно решение отличное от нуля, то положим с = 0. Тогда  =
=  . Подставляя найденное значение v (x) в исходное уравнение и учитывая, что
. Подставляя найденное значение v (x) в исходное уравнение и учитывая, что  =0, запишем
=0, запишем  =
=  или
или  , откуда после интегрирования получим
, откуда после интегрирования получим  . Окончательно общее решение запишется
. Окончательно общее решение запишется
y = u (x) v (x)  .
.
Найдем частное решение, удовлетворяющее начальному условию
 (0) = 1.
(0) = 1.  (0)
(0)  = 1. Откуда
= 1. Откуда  , тогда частное
, тогда частное
решение запишется  .
.
Для решения задачи 3 необходимо изучить пункт 3 программы.
Некоторые типы уравнений второго порядка приводятся к уравнениям первого порядка. К ним относятся:
1) Уравнения вида  , которые не содержат явным образом
, которые не содержат явным образом  . Обозначим производную
. Обозначим производную  через
через  т.е.
т.е.
 Тогда
Тогда 
Подставляя эти выражения производных в исходное уравнение, получим уравнение первого порядка.
2) Уравнения вида  , которые не содержат явным образом
, которые не содержат явным образом  .
.
Положим 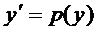 и, так как
и, так как 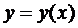
 то для определения производной
то для определения производной  применим правило дифференцирования сложной функции
применим правило дифференцирования сложной функции

Подставляя выражения производных в исходное уравнение, получим уравнение первого порядка относительно вспомогательной функции 
 .
.
Пример 5. Решить уравнение  .
.
Решение. Вводим новую функцию  ,
,  , тогда
, тогда  . Подставив ее в уравнение, имеем
. Подставив ее в уравнение, имеем
 .
.
Это линейное уравнение первого порядка относительно  и его решение разыскиваем в виде произведения
и его решение разыскиваем в виде произведения 

Учитывая требования  ,
,  , находим функцию
, находим функцию  :
:  подставляем в уравнение для определения
подставляем в уравнение для определения 

Отсюда

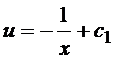 .
.
Таким образом, 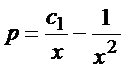 , и можно найти функцию y
, и можно найти функцию y
 ,
, 
Пример 6. Найти общий интеграл уравнения  .
.
Решение. Уравнение не содержит явным образом 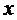 . Следовательно, допускается понижение порядка. Обозначим
. Следовательно, допускается понижение порядка. Обозначим 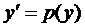
 Тогда
Тогда  .
.
Получим уравнение с разделяющимися переменными  , интегрируя которое, находим
, интегрируя которое, находим  или
или



Откуда 
Перед решением задач 4 и 5 следует изучить пункты 4, 5 програм-мы.
Пусть имеем уравнение
 , (1)
, (1)
где p и q - действительные числа.
Для уравнения с постоянными коэффициентами в некоторых случаях частное решение можно найти, не прибегая к интегрированию.
1. Пусть правая часть уравнения (1) представляет собой произведение показательной функции на многочлен, т.е. имеет вид  , где
, где  - многочлен n– й степени. Тогда возможны случаи:
- многочлен n– й степени. Тогда возможны случаи:
а) Число a не является корнем характеристического уравнения 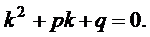 В этом случае частное решение нужно искать в виде
В этом случае частное решение нужно искать в виде
 . (2)
. (2)
Где  – многочлен степени n с неизвестными коэффициентами. Подставляя выписанное решение в уравнение (1) и приравнивая коэффициенты при одинаковых степенях х, получим систему n+1 уравнений для определения неизвестных коэффициентов
– многочлен степени n с неизвестными коэффициентами. Подставляя выписанное решение в уравнение (1) и приравнивая коэффициенты при одинаковых степенях х, получим систему n+1 уравнений для определения неизвестных коэффициентов  .
.
б) Число a есть корень характеристического уравнения кратности r. Частное решение нужно искать в виде
 .
.
2. Пусть правая часть уравнения имеет вид
 , (3)
, (3)
где  - многочлены от х. Тогда форма частного решения определяется следующим образом:
- многочлены от х. Тогда форма частного решения определяется следующим образом:
а) если a + i b не является корнем характеристического уравнения, то частное решение уравнения (1) следует искать в виде
 , (4)
, (4)
где  - многочлены, степень которых равна наивысшей степени многочленов
- многочлены, степень которых равна наивысшей степени многочленов  ;
;
б) если a + ib является корнем характеристического уравнения, то частное решение уравнения (1) следует искать в виде  .
.
Пример 7. Написать вид частного решения уравнения
 . (5)
. (5)
Решение. Определим корни характеристического уравнения для однородного уравнения
 ,
,
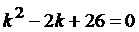 ,
,
 ,
,
 ,
, 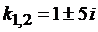 .
.
Правая часть уравнения (5) является суммой функций, поэтому частное решение имеет вид 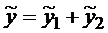 , где
, где  – частное решение уравнения
– частное решение уравнения
 ,
,
 – частное решение уравнения
– частное решение уравнения
 .
.
В нашем случае 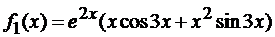 – это функция специального вида (3). Имеем
– это функция специального вида (3). Имеем  не совпадают с корнями
не совпадают с корнями 
 и поэтому
и поэтому  . Поскольку
. Поскольку  ,то
,то  , поэтому
, поэтому  , а это означает, что
, а это означает, что  будут полными многочленами второй степени:
будут полными многочленами второй степени:  . По формуле (4) имеем
. По формуле (4) имеем

Отметим, что  является функцией вида (2), где
является функцией вида (2), где  . Следовательно,
. Следовательно,
 ,
,
так как  не является корнем характеристического уравнения, т.е.
не является корнем характеристического уравнения, т.е.  . Таким образом, частное решение уравнения (5) будет иметь вид
. Таким образом, частное решение уравнения (5) будет иметь вид

Пример 8. Найти общее решение уравнения.

Решение. Общее решение будет иметь вид  .
.
Найдем общее решение соответствующего однородного уравнения. Составим характеристическое уравнение и найдем его корни
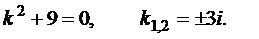
Тогда общее решение соответствующего однородного уравнения
 .
.
Правая часть данного неоднородного уравнения  имеет вид
имеет вид  . Так как коэффициент 3 в показателе степени не является корнем характеристического уравнения, то частное решение будем искать в форме
. Так как коэффициент 3 в показателе степени не является корнем характеристического уравнения, то частное решение будем искать в форме  , т.е. положим
, т.е. положим  . Подставляя это выражение в заданное уравнение, будем иметь
. Подставляя это выражение в заданное уравнение, будем иметь
 .
.
Сокращая на  и приравнивая коэффициенты при одинаковых степенях х, получим
и приравнивая коэффициенты при одинаковых степенях х, получим

откуда  Следовательно, частное решение будет иметь вид
Следовательно, частное решение будет иметь вид 
Общее решение: 

Пример 9. Найти общее решение уравнения.

Решение. Общее решение будет иметь вид  . Общее решение соответствующего однородного уравнения
. Общее решение соответствующего однородного уравнения
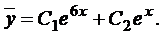
Правая часть данного неоднородного уравнения 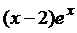 имеет вид
имеет вид 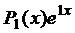 . Так как коэффициент 1 в показателе степени является простым корнем характеристического уравнения, то частное решение будем искать в форме
. Так как коэффициент 1 в показателе степени является простым корнем характеристического уравнения, то частное решение будем искать в форме  . Подставляя это выражение в заданное уравнение, будем иметь
. Подставляя это выражение в заданное уравнение, будем иметь
 или
или 
Сокращая на 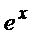 и приравнивая коэффициенты при одинаковых степенях х, получим
и приравнивая коэффициенты при одинаковых степенях х, получим  откуда
откуда 
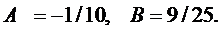 Следовательно, частное решение будет
Следовательно, частное решение будет

Общее решение:  +
+ 
Пример 10. Найти общее решение дифференциального уравнения
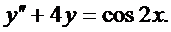
Решение. Общее решение будет иметь вид  .
.
Найдем общее решение соответствующего однородного уравнения
Составим характеристическое уравнение и найдем его корни

Общее решение соответствующего однородного уравнения
 .
.
Правая часть данного неоднородного уравнения  , очевидно, что bi =2i является корнем характеристического уравнения, частное решение будем искать в форме
, очевидно, что bi =2i является корнем характеристического уравнения, частное решение будем искать в форме

где А и В – неизвестные коэффициенты.
Найдем производные  :
:


Подставляя выражения  и производных в заданное уравнение и приравнивая коэффициенты при
и производных в заданное уравнение и приравнивая коэффициенты при  и
и  , получим два уравнения для определения А и В:
, получим два уравнения для определения А и В:
 .
.
Откуда  Следовательно, частное решение
Следовательно, частное решение  . Общее решение будет иметь вид
. Общее решение будет иметь вид
 +
+  .
.
Пример 11. Найти общее решение линейного неоднородного уравнения

Решение. Общее решение будет иметь вид  .
.
Найдем общее решение соответствующего однородного уравнения. Составим характеристическое уравнение и найдем его корни

Общее решение соответствующего однородного уравнения
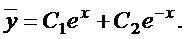 .
.
 2018-02-12
2018-02-12 190
190








