2018-02-14
511
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: mb и ma.
, 
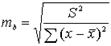(8.2)
где S2 – остаточная дисперсия на одну степень свободы.
Величина стандартной ошибки совместно с t -распределением Стьюдента при n -2 степенях свободы применяется для проверки существенности коэффициента регрессии.
При гипотезе Н0: b - b0 =0, t -статистика выглядит следующим образом:
Значение сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n -2).
Если фактическое значение t -критерия превышает табличное, то гипотезу о несущественности коэффициента регрессии можно отклонить.
Процедура оценивания существенности параметра а не отличается от уже рассмотренной для коэффициента регрессии.
Взаимосвязь t-статистики и F-статистики для парной регрессии.
Существует связь между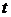 
-критерием Стьюдента и 
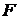-критерием Фишера: 
. В прогнозных расчетах по уравнению регрессии определяется предсказываемое 
значение как точечный прогноз 
при 
, т.е. путем подстановки в уравнение регрессии 
соответствующего значения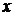 
. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки , т.е. 
, и соответственно интервальной оценкой прогнозного значения :
|
|
|
,
где 
, а 
– средняя ошибка прогнозируемого индивидуального значения:
.
