Вводим данные в таблицу

 

yi	(y-yi)/y	Ai
681,270 673,026 681,606 675,381 678,241 678,746 678,241 681,102 677,064 678,746 672,521 668,652 672,353 677,737 677,568 678,746	-0,108 0,074 -0,167 0,103 0,041 -0,033 -0,037 0,017 0,038 0,130 0,190 -0,207 -0,201 -0,244 -0,008 0,147	0,108 0,074 0,167 0,103 0,041 0,033 0,037 0,017 0,038 0,130 0,190 0,207 0,201 0,244 0,008 0,147 1,745

 

2. Рассчитаем параметры уравнения y=a₀+a₁x с помощью статистической функции ЛИНЕЙН. Получаем следующую статистику:

 

        

 

А1	-0,168	729,891	А0
Случ.ош. а1	1,093	345,080	Случ. Ош. А0
R2	0,002	91,741	Sост.
Fфакт.	0,023	14	Число степеней свободы
	199,073	117829,864

        

Уравнение парной линейной регрессии имеет вид:

 

У=729-0,17х

 

    Экономический смысл уравнения: при увеличении потребительских расходов в расчете на душу населения по районам на 1 тыс. руб. - средняя заработная плата и выплаты социального характера уменьшается в среднем на 0,17 тыс. руб.

 

        

3. Рассчитаем коэффициент корреляции:

-по формуле:

-с помощью статистической функции КОРРЕЛ-

 

    При таком значении коэффициент корреляции линейная связь между величинами x и y практически отсутствует. Поэтому вышеприведенное уравнение не имеет смысл, т.е. средняя заработная плата и выплаты социального характера по районам не связаны с потребительскими расходами.

 

    4. Средняя ошибка аппроксимации рассчитывается по формуле:

 

.

 

    Полученное значение средняя ошибка аппроксимации 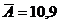%. Это означает, что в среднем, расчетные значения модели отклоняются от фактических значений на 10,9%, что подтверждает низкое качество модели.

Коэффициент детерминации, рассчитанный с помощью функции ЛИНЕЙН, равен R² = 0,001687, что также не подтверждает связь между средней заработной платой и выплатами социального характера по районам с потребительскими расходами. Т.е. точность подбора уравнения регрессии составляет в среднем 0,17%

 

 

    5. Оценка статистической значимости по критерию Фишера.

 Выдвигаем нулевую гипотезу о статистически незначимом отличии показателей от нуля: a₀=а₁=r_xy=0.

 Табличное значение критерия Фишера для заданного уровня значимости  и числа степеней свободы ν=14 (ν=n-m-1, где n=16 – число измерений, m=1 – число независимых переменных) равно F_табл = 4,60.

 Если F_табл > F_факт, то нулевая гипотеза не отвергается. В данном случае F_факт =0,024, а F_табл = 4,60. Т.е. полученный результат статистически не значим.

Сравниваем фактические значения t-критерия с табличным значением:

=2,145

 

;

;

.

 

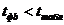Нулевую гипотезу для параметров принимаем. Их нельзя считать статистически значимыми и надежными.

Поскольку модель отвергается, рассчитывать доверительные интервалы для параметров регрессии не имеет смысла.

Выводы:

5. Средняя заработная плата и выплаты социального характера по регионам не связаны с прожиточным минимумом. Поскольку модель отвергнута, не имеет смысл рассчитывать по ней прогнозные значения.

Задание №4

ЗАДАЧА:

          Представлена сравнительная таблица данных:

- денежные доходы на душу населения

- потребительские расходы на душу населения.

 

Район	потр.расх. на д/н. Х	ден.доходы на д/н. У
Бурятия	524	408
Тыва	371	249
Хакасия	453	253
Краснодарский край	1006	580
Иркутская обл.	997	651
Усть - Ордынский авт.окр.	217	139
Читинская обл.	486	322
Саха	1989	899
Еврейский авт.окр.	595	330
Чукотский авт.окр.	1550	446
Приморский край	937	642
Хабаровский край	761	542
Амурская обл.	767	504
Камчатская обл.	1720	861
Магаданская обл.	1735	707
Сахалинская обл.	1052	557

ТРЕБУЕТСЯ:

6. Рассчитать параметры уравнения линейной регрессии.

7. Оценить статистическую надежность регрессионного моделирования с помощью критерия Фишера.

8. Оценить статистическую надежность регрессионного моделирования с помощью t-критерия Стьюдента.

9. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости =0,05.

10. Оценить полученные результаты и сделать выводы.

РЕШЕНИЕ:

1.1. Вводим данные в таблицу Excel:

 

потр.расходы на д/н. Х	ден.доходы на душу нас. У	yi	(y-yi)/y	|(y-yi)/y|	|(y-yi)/y|*100
524	408	356,146	0,127	0,127	12,709
371	249	302,143	-0,213	0,213	21,343
453	253	331,086	-0,309	0,309	30,864
1006	580	526,273	0,093	0,093	9,263
997	651	523,097	0,196	0,196	19,647
217	139	247,787	-0,783	0,783	78,264
486	322	342,733	-0,064	0,064	6,439
1989	899	873,234	0,029	0,029	2,866
595	330	381,206	-0,155	0,155	15,517
1550	446	718,284	-0,611	0,611	61,050
937	642	501,919	0,218	0,218	21,819
761	542	439,798	0,189	0,189	18,857
767	504	441,916	0,123	0,123	12,318
1720	861	778,287	0,096	0,096	9,607
1735	707	783,582	-0,108	0,108	10,832
1052	557	542,509	0,026	0,026	2,602

 

 

1.2. Рассчитаем параметры уравнения y=a₀+a₁x с помощью статистической функции ЛИНЕЙН. Получаем следующую статистику:

 

 

а1	0,353	171,194	а0
случ.ошибка а1	0,0523	56,569	случ.ошибка а0
R2	0,765	109,343	S2
Fфакт.	45,598	14	число степеней свободы
	545169,843	167383,907

 

 Уравнение парной линейной регрессии имеет вид:

y=171,19+0,35х

Экономический смысл уравнения: при увеличении потребительских расходов в расчете на душу населения по районам на 1 тыс. руб. – денежный доход на душу населения увеличился в среднем на 0,35 тыс. руб.

2.1. Рассчитаем коэффициент корреляции:

-по формуле: r_xy = a*(σx/σy)= 0.35*(171.19/211.03) = 0.29

-с помощью статистической функции КОРРЕЛ-rxy.= 0.29

        При таком значении коэффициент корреляции линейная связь между величинами x и y средняя. Поэтому вышеприведенное уравнение имеет смысл, т.е. средняя заработная плата и выплаты социального характера по районам связаны с потребительскими расходами.

2.2. Средняя ошибка аппроксимации рассчитывается по формуле:

 

.

 

Полученное значение средняя ошибка аппроксимации A cp=20.87%. Это означает, что в среднем, расчетные значения модели отклоняются от фактических значений на 14,03%, что подтверждает низкое качество модели.

2.3. Коэффициент детерминации, рассчитанный с помощью функции ЛИНЕЙН, равен R² = 0,70509 что также подтверждает связь между денежными доходами и потребительскими расходами населения. Т.е. точность подбора уравнения регрессии составляет в среднем 70,5%.