Оценка статистической значимости по критерию Стьюдента

Задание №1

ЗАДАЧА

Представлена сравнительная таблица данных:

- средняя заработная плата и выплаты социального характера;

-потребительские расходы на душу населения.

 

	Потребительские расходы	Средняя зар.плата и
Район	на душу населения, тыс. руб., Y	выплаты соц. хар-ра, тыс. руб., X
Респ. Марий Эл	302	554
Респ. Мордовия	360	560
Чувашская респ.	310	545
Кировская обл.	415	672
Нижегородская обл.	452	796
Белогородская обл.	502	777
Воронежская обл.	355	632
Курская обл.	416	688
Липецкая обл.	501	833
Тамбовская обл.	403	577
Респ. Калмыкия	208	584
Респ. Татарстан	462	949
Архангельская обл.	368	888
Волгоградская обл.	399	831
Пензенская обл.	342	562
Саратовская обл.	354	665
Ульяновская обл.	558	705
Fтабл.=4,54 (α=0,05)	sy=82,89	sx=125,16

ТРЕБУЕТСЯ:

1. Рассчитать параметры уравнения линейной регрессии.
2. Оценить статистическую надежность регрессионного моделирования с помощью критерия Фишера.
3. Оценить статистическую надежность регрессионного моделирования с помощью t-критерия Стьюдента.
4. рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости =0,05.
5. Оценить полученные результаты и сделать выводы.

РЕШЕНИЕ:

1.

1.1. Вводим данные в таблицу Excel:

 

№	y	X	yi	(y-yi)/y	Ai
1	302	554	339,539	-0,124	0,124
2	360	560	341,876	0,050	0,050
3	310	545	336,033	-0,084	0,084
4	415	672	385,502	0,071	0,071
5	452	796	433,802	0,040	0,040
6	502	777	426,401	0,151	0,151
7	355	632	369,921	-0,042	0,042
8	416	688	391,734	0,058	0,058
9	501	833	448,214	0,105	0,105
10	403	577	348,498	0,135	0,135
11	208	584	351,224	-0,689	0,689
12	462	949	493,398	-0,068	0,068
13	368	888	469,637	-0,276	0,276
14	399	831	447,435	-0,121	0,121
15	342	562	342,655	-0,002	0,002
16	354	665	382,775	-0,081	0,0813
итого	6707	11818			2,385
среднее	394,529	695,176			0,140
σ	82,89	125,16
σ2	6870,75	15665,026

 

       1.2. Рассчитаем параметры уравнения y=a₀+a₁x с помощью статистической функции ЛИНЕЙН. Получаем следующую статистику:

А1	0,38951557	123,7473528	А0
Случайная ошибка А1	0,138284595	97,67787942	Случайная ошибка А0
R2	0,345954374	71,36295341	S остатков
F фактическая	7,934179833	15	число степеней свободы
	40406,1685	76390,0668

 

Уравнение парной линейной регрессии имеет вид:

 

y=123,75+0,39x

 

       Экономический смысл уравнения: при увеличении потребительских расходов в расчете на душу населения по районам на 1 тыс. руб. - средняя заработная плата и выплаты социального характера увеличиваются в среднем на 0,39 тыс. руб.

 

       2.

       2.1. Рассчитаем коэффициент корреляции:

-по формуле: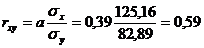

-с помощью статистической функции КОРРЕЛ- .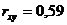

       При таком значении коэффициент корреляции линейная связь между величинами x и y средняя. Поэтому вышеприведенное уравнение имеет смысл, т.е. средняя заработная плата и выплаты социального характера по районам связаны с потребительскими расходами.

       2.2. Средняя ошибка аппроксимации рассчитывается по формуле:

 

.

 

Полученное значение средняя ошибка аппроксимации 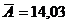%. Это означает, что в среднем, расчетные значения модели отклоняются от фактических значений на 14,03%, что подтверждает низкое качество модели.

       2.3. Коэффициент детерминации, рассчитанный с помощью функции ЛИНЕЙН, равен R² = 0,345954374, что также подтверждает связь между средней заработной платой и выплатами социального характера по районам с потребительскими расходами. Т.е. точность подбора уравнения регрессии составляет в среднем 34,6%.

 

       3. Оценка статистической значимости по критерию Фишера.

3.1. Выдвигаем нулевую гипотезу о статистически незначимом отличии показателей от нуля: a₀=а₁=r_xy=0.

3.2. Табличное значение критерия Фишера для заданного уровня значимости  и числа степеней свободы ν=15 (ν=n-m-1, где n=17 – число измерений, m=1 – число независимых переменных) равно F_табл = 4,54.

3.3. Если F_факт > F_табл, то нулевая гипотеза отвергается. В данном случае F_факт = 7,93, а F_табл = 4,54. Т.е. полученный результат статистически значим с вероятностью 0,95. Эти данным можно доверять, т.к. надежность модели составляет 95%, а ошибка – 5%.

 

Оценка статистической значимости по критерию Стьюдента.

 

3.1. Выдвигаем нулевую гипотезу о статистически незначимом отличии показателей от нуля: a₀=а₁=r_xy=0.

3.2. Табличное значение t-критерия для заданного уровня значимости  и числа степеней свободы ν=15 (ν=n-m-1, где n=17 – число измерений, m=1 – число независимых переменных) равно t_табл = 2,131.

3.3. Рассчитаем фактические значения t-критерия для каждого параметра модели. С этой целью определим случайные ошибки параметров m_a0, m_а1, m_rxy.

       Значения m_a0, m_a1 с помощью функции ЛИНЕЙН:

 

m_a0= 97,68,  m_a1 =0,14.

Значение m_rxy рассчитаем по формуле:

.

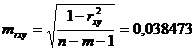Тогда фактические значения t-критерия равны:

,

,

.

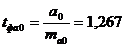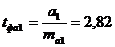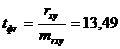3.4. Сравниваем фактические значения t-критерия с табличным значением:

;

;

.

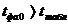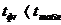Нулевую гипотезу принимаем частично. Значение а₀ можно считать статистически значимыми и надежными, в то время как значение а₁ – мало надежно.

 

3.5. В целом модель не отвергается, поэтому  рассчитаем доверительные интервалы для параметров регрессии.

 

Для значения а₀:

 

 

,

 

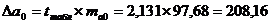
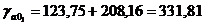
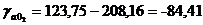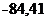
т.е. доверительный интервал для 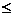а₀

а₀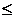

 

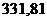
Для значения а₁:

 

 

 

,

 

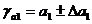
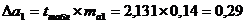
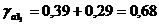
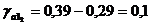 т.е. доверительный интервал для а₁:

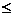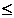0,1 а₁ 0,68

 

       Анализ границ измерения коэффициентов регрессии свидетельствует о том, что коэффициенты статистически значимы, поскольку они не принимают нулевых значений с вероятностью 95% за исключением коэффициента а₀, т.к. он выходит за область значений меньше нуля. Т.к. нас интересует область значений больше нуля, то коэффициент а₀ особого значения не имеет. Таким образом,  нулевую гипотезу мы можем отвергнуть.

       Но уравнение регрессии описывает лишь 34,6% модели и поэтому полностью доверять модели мы не можем, т.к. некоторые коэффициенты не надежны.

 

       3.6. С помощью полученных оценок уравнения регрессии рассчитаем прогнозные значения. Выполним прогноз при прогнозном значении х=107% от среднего уровня.

       Рассчитаем прогнозное значение средней зар. платы и выплаты соц. хар-ра (Х_р):

 

 

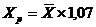
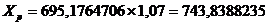
Рассчитаем прогнозное значение потребительских расходов на душу населения (Y_р):

 

 

 

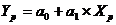
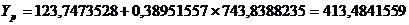
Найдем случайную ошибку прогнозного значения потребительских расходов на душу населения (mY_р):

 

 

 

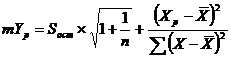
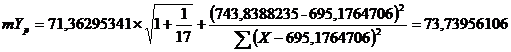
       Теперь рассчитаем доверительный интервал прогнозного значения потребительских расходов на душу населения (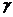 Yp):

 

 

 

 

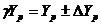
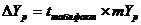
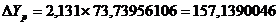
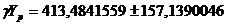
Тогда соответственно доверительный интервал прогнозного значения равен:

 

 

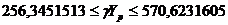
       Изобразим полученные результаты на графике:

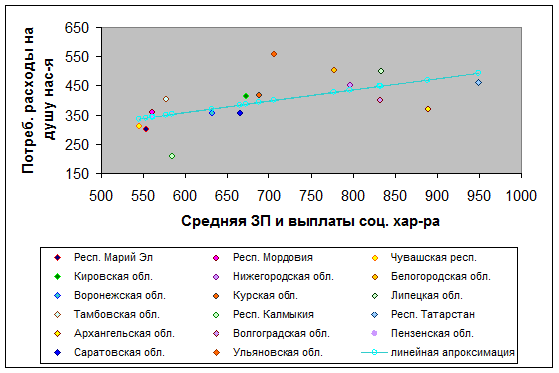
       Выводы:

1. Средняя заработная плата и выплаты социального характера по регионам не связаны с прожиточным минимумом.
2. Поскольку модель отвергнута, не имеет смысл рассчитывать по ней прогнозные значения.

Задание №2

Представлена сравнительная таблица данных:

- средняя заработная плата и выплаты социального характера;

-потребительские расходы на душу населения.

 

район	потреб. р-ды на душу нас, у	ден. д-ды на душу нас., х
Респ. Башкортостан	461	632
Респ. Удмуртия	524	738
Курганская обл.	298	515
Оренбургская обл.	351	640
Пермская обл.	624	942
Свердлоская обл.	584	888
Челябинская обл.	425	704
Респ. Алтай	277	603
Алтайский край	321	439
Кемеровская обл.	573	985
Новосибирская обл	576	735
Омская обл.	588	760
Томская обл.	497	830
Тюменская обл	863	2093
Fтабл=4,75 (a=0,05)	sу=152,47	sх=382,79

ТРЕБУЕТСЯ:

1. Рассчитать параметры уравнения линейной регрессии.
2. Оценить статистическую надежность регрессионного моделирования с помощью критерия Фишера.
3. Оценить статистическую надежность регрессионного моделирования с помощью t-критерия Стьюдента.
4. рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости =0,05.
5. Оценить полученные результаты и сделать выводы.

РЕШЕНИЕ:

1.

1.1. Вводим данные в таблицу Excel:

 

№	y	x	yi	(y-yi)/y	Ai
1	461	632	848,280	-0,840	0,840
2	524	738	954,280	-0,821	0,821
3	298	515	731,280	-1,454	1,454
4	351	640	856,280	-1,440	1,440
5	624	942	1158,280	-0,856	0,856
6	584	888	1104,280	-0,891	0,891
7	425	704	920,280	-1,165	1,165
8	277	603	819,280	-1,958	1,958
9	321	439	655,280	-1,041	1,041
10	573	985	1201,280	-1,096	1,096
11	576	735	951,280	-0,652	0,652
12	588	760	976,280	-0,660	0,660
13	497	830	1046,280	-1,105	1,105
14	863	2093	2309,280	-1,676	1,676
итого	6962	11504			15,65
среднее	497,286	821,714			1,118
σ	152,47	382,79
σ2	23247,10	146528,184

 

       1.2. Рассчитаем параметры уравнения y=a₀+a₁x с помощью статистической функции ЛИНЕЙН. Получаем следующую статистику:

 

а1	0,342391549	215,9376873	а0
случ.ошибка а1	0,058751906	53,25849747	случ. ошибка а0
R^2	0,738918707	84,14751571	S остаток
Fфакт	33,96269558	12	n-m-1
	240483,2043	84969,65281

 

Уравнение парной линейной регрессии имеет вид:

 

y=215,94 + 0,34x

 

       Экономический смысл уравнения: при увеличении потребительских расходов в расчете на душу населения по районам на 1 тыс. руб. - средняя заработная плата и выплаты социального характера увеличиваются в среднем на 0,34 тыс. руб.

 

       2.

       2.1. Рассчитаем коэффициент корреляции:

-по формуле: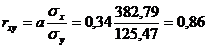

-с помощью статистической функции КОРРЕЛ- .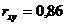

       При таком значении коэффициент корреляции линейная связь между величинами x и y средняя. Поэтому вышеприведенное уравнение имеет смысл, т.е. средняя заработная плата и выплаты социального характера по районам связаны с потребительскими расходами.

       2.2. Средняя ошибка аппроксимации рассчитывается по формуле:

 

.

 

Полученное значение средняя ошибка аппроксимации %. Это означает, что в среднем, расчетные значения модели отклоняются от фактических значений на 111,83%, что подтверждает низкое качество модели.

       2.3. Коэффициент детерминации, рассчитанный с помощью функции ЛИНЕЙН, равен R² = 0,738918707, что также подтверждает связь между средней заработной платой и выплатами социального характера по районам с потребительскими расходами. Т.е. точность подбора уравнения регрессии составляет в среднем 73,89%.

 

       3. Оценка статистической значимости по критерию Фишера.

3.1. Выдвигаем нулевую гипотезу о статистически незначимом отличии показателей от нуля: a₀=а₁=r_xy=0.

3.2. Табличное значение критерия Фишера для заданного уровня значимости  и числа степеней свободы ν=12 (ν=n-m-1, где n=14 – число измерений, m=1 – число независимых переменных) равно F_табл = 4,54.

3.3. Если F_факт > F_табл, то нулевая гипотеза отвергается. В данном случае F_факт = 33,96, а F_табл = 4,54. Т.е. полученный результат статистически значим с вероятностью 0,95. Эти данным можно доверять, т.к. надежность модели составляет 95%, а ошибка – 5%.