Рассмотрим задачу анализа динамики бруса батана и рапирного механизма с учетом упругости элементов их привода. Для кулачково-рычажных батанных и рапирных механизмов металлоткацких станков типа СТР динамическая модель будет состоять из четырех взаимосвязанных контуров: I - главного вала, как крутильно-колеблющейся системы с конечным числом степеней свободы; II- промежуточного вала, так же крутильно-колеблющейся системы с конечным числом степеней свободы; III - бруса батана, изгибно-колеблющейся системы с распределенными параметрами; IV – контур рапирного механизма, как крутильно-колеблющейся системы с конечным числом степеней свободы. Контуры I, II и IV связаны между собой кулачковой передачей, II и III – стержневой.
Остановимся на станках типа СТР, имеющих n-коробочный привод батана. Путем упрощений по методу Е.И. Ривина [121] динамическую модель упругой системы батанного и рапирного механизмов можно привести к виду, показанному на рис. 4.7.
Обозначим через 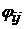 - абсолютные угловые перемещения дисков (i – номер контура, j – номер диска);
- абсолютные угловые перемещения дисков (i – номер контура, j – номер диска); 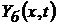 - абсолютные перемещения сечений бруса;
- абсолютные перемещения сечений бруса; 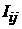 - моменты инерции масс дисков, отражающих инерционные свойства реальной конструкции;
- моменты инерции масс дисков, отражающих инерционные свойства реальной конструкции; 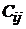 - коэффициенты жесткости упругих элементов;
- коэффициенты жесткости упругих элементов; 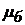 - погонная масса бруса;
- погонная масса бруса; 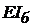 - изгибная жесткость бруса;
- изгибная жесткость бруса; 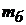 - приведенная масса лопасти и подбатанного вала;
- приведенная масса лопасти и подбатанного вала; 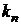 - коэффициент постели;
- коэффициент постели; 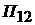 ,
, 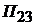 - функции перемещения кулачкового и стержневого механизмов соответственно;
- функции перемещения кулачкового и стержневого механизмов соответственно; 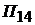 - передаточная функция, учитывающая линейную жесткость (
- передаточная функция, учитывающая линейную жесткость (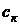 ) и линейное сопротивление (
) и линейное сопротивление (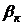 ) клиноременной передачи, рис. 4.1,в;
) клиноременной передачи, рис. 4.1,в;
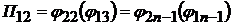 ;
; 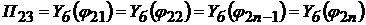 ;
;
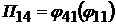 ;
; 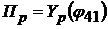 ;
;
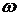 - угловая скорость вращения главного вала, здесь принимаем величиной постоянной.
- угловая скорость вращения главного вала, здесь принимаем величиной постоянной.
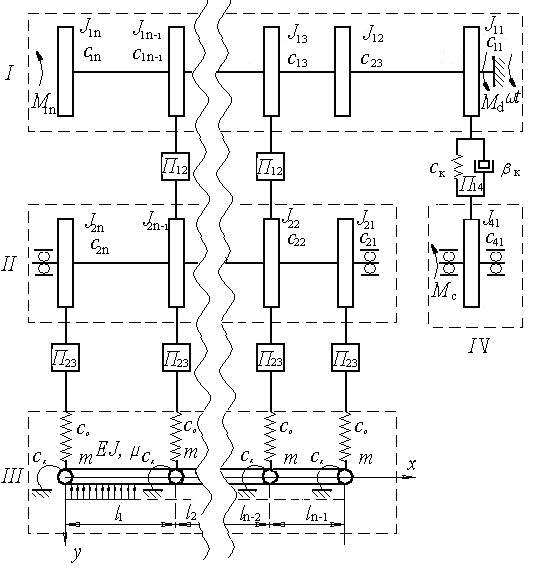
Рис.4.7. Динамическая модель кулачково-рычажных батанного и рапирного
механизмов при учете упругости элементов привода
С целью упрощения математической модели примем допущение, что деформируемые элементы являются идеально упругими, то есть не обладают диссипативными свойствами. Для решения ряда вопросов это допущение вполне приемлемо. В этом случае движение системы будет описываться следующими дифференциальными уравнениями:
 контур 1 (главный вал)
контур 1 (главный вал)
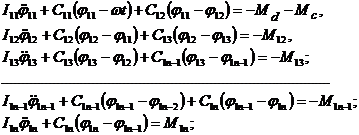 (4.11) (4.11)
|
контур 2 (промежуточный вал)
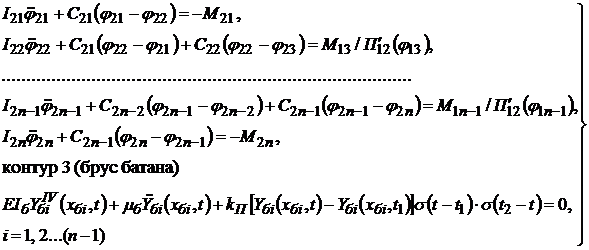 (4.12)
контур 4 (рапирный механизм - считаем, что все звенья механизма считаются абсолютно жесткими и учитываем податливость только клиноременной передачи) (4.12)
контур 4 (рапирный механизм - считаем, что все звенья механизма считаются абсолютно жесткими и учитываем податливость только клиноременной передачи)
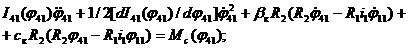 (4.13) (4.13)
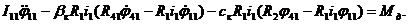
|
Здесь:
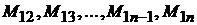 - моменты сопротивления, действующие на главный вал со стороны промежуточного;
- моменты сопротивления, действующие на главный вал со стороны промежуточного;
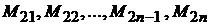 - моменты сопротивления, действующие на про-
- моменты сопротивления, действующие на про-
межуточный вал со стороны батана;
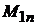 - момент сил сопротивления со стороны механизмов зевообразования,
- момент сил сопротивления со стороны механизмов зевообразования,
отпуска основы, набора товара;
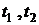 - время цикла, соответствующее подходу берда к опушке ткани и отходу от нее;
- время цикла, соответствующее подходу берда к опушке ткани и отходу от нее;
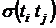 - единичные функции Хевисайда [122];
- единичные функции Хевисайда [122];
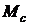 -приведенный к валу двигателя момент сопротивления со стороны рапирного механизма;
-приведенный к валу двигателя момент сопротивления со стороны рапирного механизма;
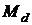 - движущий момент на валу двигателя.
- движущий момент на валу двигателя.
Уравнения (4.11) и (4.12) должны удовлетворять условиям в концевых сечениях бруса и условиям сопряжения участков. В качестве примера этих граничных условий рассмотрим брус батана с тремя лопастями, рис. 4.8, (металлоткацкий станок СТР-130-М).
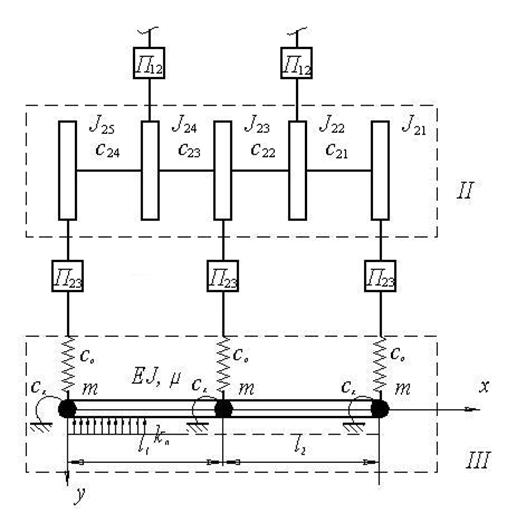
Рис.4.8. Динамическая модель трехлопастного кулачково-рычажного
батанного механизма при учете упругости элементов привода
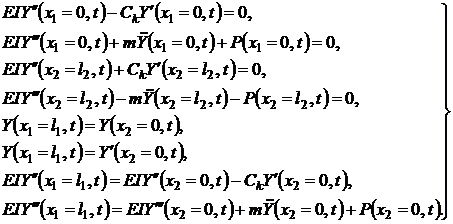
| (4.14) |
где 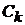 - приведенная к изгибной крутильная жесткость лопастей с учетом жесткости подбатанного вала и его опор;
- приведенная к изгибной крутильная жесткость лопастей с учетом жесткости подбатанного вала и его опор;
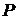 - усилия, действующие на сечение бруса со стороны привода и определяемые деформациями упругих элементов, отражающих деформационные свойства шарнирных соединений стержневой части привода.
- усилия, действующие на сечение бруса со стороны привода и определяемые деформациями упругих элементов, отражающих деформационные свойства шарнирных соединений стержневой части привода.
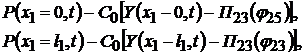
| (4.15) |
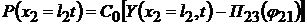 . .
|
Очевидно, что
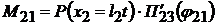 , , 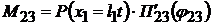 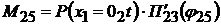 . .
|
Введем в рассмотрение относительные координаты
|
| ||
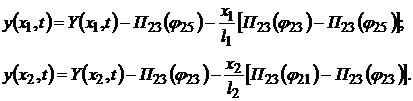
| (4.16) | |
Второе и третье слагаемые первой части двух последних выражений представляют собой переносное движение сечений бруса (возмущающая функция). Кроме кинематического перемещения они учитывают перемещение сечений бруса вследствие деформаций звеньев приводной системы.
Согласно [84] функции перемещения П и передаточные функции 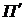 и
и 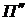 можно линеаризировать, разложив их в ряд Тейлора и ограничившись удержанием первых двух членов этого ряда
можно линеаризировать, разложив их в ряд Тейлора и ограничившись удержанием первых двух членов этого ряда
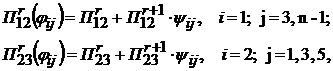
| (4.17) |
где r - 0, 1, 2 – порядок производной;
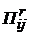 - функции от кинематических значений параметра
- функции от кинематических значений параметра 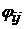 .
.
Имея в виду (4.15), (4.16), (4.17) и отбрасывая в функциях возмущения члены второго порядка малости, системы (4.11), (4.12) можно привести к виду:
для главного и промежуточного валов
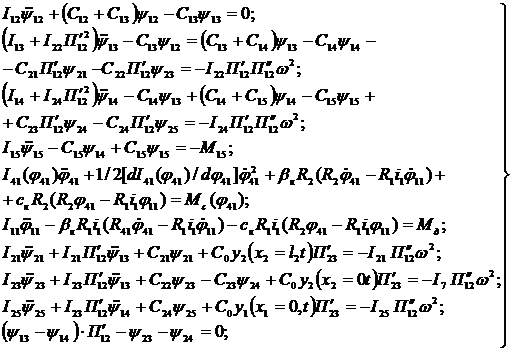
| (4.18) |
для бруса батана
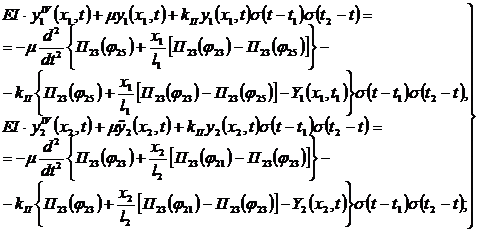
| (4.19) |
Для условий сопряжения
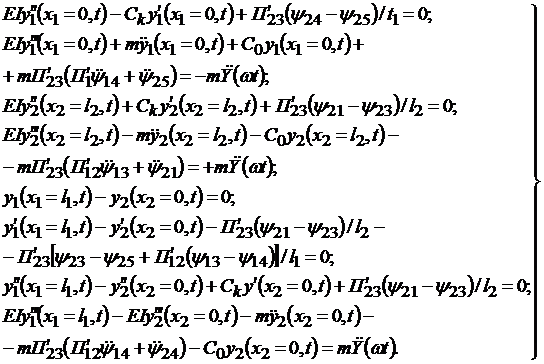
| (4.20) |
Уравнения (4.18), (4.19) и (4.20) представляют собой систему дифференциальных уравнений с переменными коэффициентами. Решение этой системы можно получить с помощью метода условного осциллятора [84].
Рассмотрим систему однородных уравнений, полученную из (4.18) и (4.20) при нулевых правых частях. Предположим, что частное решение этой системы имеет тот же вид, что и системы с постоянными коэффициентами
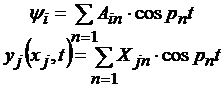
| (4.21) |
На основании (4.19) уравнение форм изгибных колебаний бруса в этом случае будет иметь вид
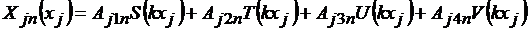
| (4.22) |
Подставляя (4.21) и (4.22) в указанную систему однородных уравнений получим систему алгебраических уравнений (4.23) относительно неизвестных амплитуд 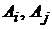 .
.

| (4.23) |
Приравнивая нулю определитель, составленный из коэффициентов при неизвестных системы (4.23), получим формальное частное уравнение, из которого определяются зависимости 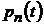 корней этого уравнения от времени.
корней этого уравнения от времени.
И.И.Вульфсоном показано [84], что если выполняется условие
 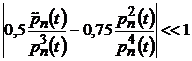
| (4.24) |
то рассматриваемую систему можно отнести к системам с медленно изменяющимися параметрами. В этом случае, следуя методу условного осциллятора решение однородной системы уравнений принимают в виде
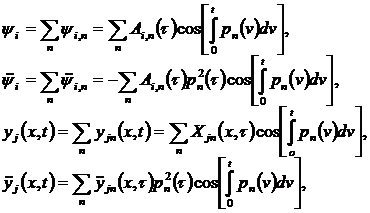
| (4.25) |
где 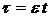 - медленное время;
- медленное время;
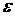 - малый параметр.
- малый параметр.
Причем, один из амплитудных коэффициентов на каждой форме, например 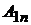 , принимают равным
, принимают равным
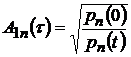
| (4.26) |
Для определения коэффициентов 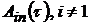 , решение (4.25) с учетом (4.22) необходимо подставить в систему однородных уравнений, полученную из (4.18) и (4.20). Поскольку
, решение (4.25) с учетом (4.22) необходимо подставить в систему однородных уравнений, полученную из (4.18) и (4.20). Поскольку 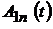 и
и 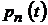 известны, то имеющаяся система позволит определить все остальные коэффициенты форм упругих колебаний рассматриваемой модели.
известны, то имеющаяся система позволит определить все остальные коэффициенты форм упругих колебаний рассматриваемой модели.
Решение уравнений вынужденных колебаний (4.18), (4.19) ищется в виде разложения искомых функций в ряд по собственным формам
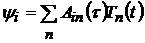 , ,
| (4.27) |
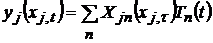 . .
|
Раскроем с учетом (4.17) правую часть первого уравнения системы (4.19), обозначив ее через 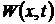 . Будем иметь
. Будем иметь
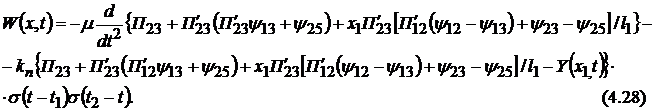
|
Разложим возмущающую функцию 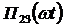 в ряд по собственным формам колебаний бруса
в ряд по собственным формам колебаний бруса
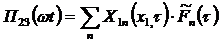 . .
|
Из условия ортогональности нормальных форм получим
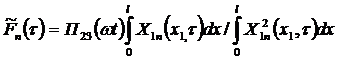 , ,
|
то есть, опуская аргументы в правой части
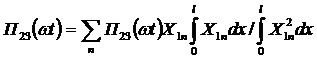 . .
| (4.29) |
Аналогично будем иметь
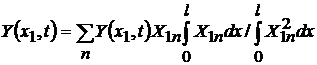 . .
| (4.30) |
Если подставить в первое уравнение системы (4.19), заменив правую часть выражением (4.28), решение (4.27) и значения (4.29), (4.30) функций 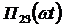 и
и 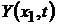 ,то для определения значений неизвестных функций
,то для определения значений неизвестных функций 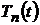 , принимая во внимание выражение (4.22) и, что
, принимая во внимание выражение (4.22) и, что 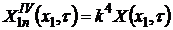 , получим уравнение
, получим уравнение
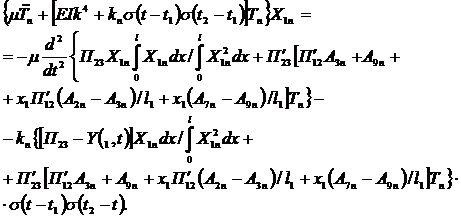
| (4.31) |
После двукратного дифференцирования соответствующих слагаемых правой части уравнение (4.31) сводится к виду
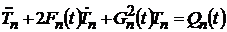 . (4.32)
. (4.32)
Произведем в уравнении (4.32) замену переменных
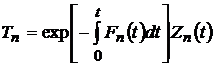 . .
| (4.33) |
Подставив (4.33) в (4.32) и поделив полученное на 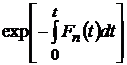 находим
находим
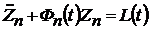 , ,
| (4.34) |
| где | |
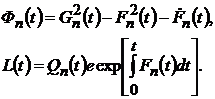
|
Общее решение уравнения (4.34) может быть представлено в виде суммы общего решения однородного уравнения
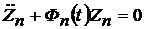
| (4.35) |
и частного уравнения (4.34), то есть
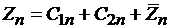 , ,
| (4.36) |
где 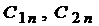 - произвольные постоянные, удовлетворяющие начальным ус-
- произвольные постоянные, удовлетворяющие начальным ус-
ловиям;
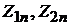 - линейно независимые решения уравнения (4.35);
- линейно независимые решения уравнения (4.35);
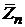 - частное решение уравнения (4.34).
- частное решение уравнения (4.34).
Решения уравнения (4.35) имеют вид
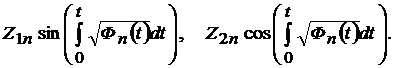
| (4.37) |
Частотное уравнение 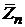 - может быть найдено методом вариации произвольных постоянных. Будем иметь
- может быть найдено методом вариации произвольных постоянных. Будем иметь
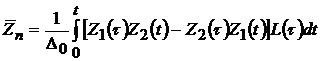 , ,
| (4.38) |
где 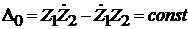 .
.
Решение (4.36) найдено, тем самым найдены и решения (4.33), (4.27). Согласно четвертому уравнению системы (4.18)
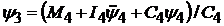 .
При необходимости учета влияния технологического сопротивления .
При необходимости учета влияния технологического сопротивления 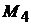 на вибрацию бруса батана зависимость
на вибрацию бруса батана зависимость 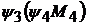 необходимо подставить в необходимо подставить в
|
выражение (4.28). Соответствующим образом изменяется и правая часть уравнения (4.31).
 2018-02-13
2018-02-13 436
436

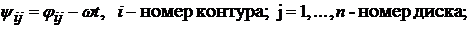 ;
;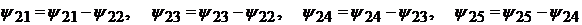 ;
;






