Построения, сделанные выше, можно выполнить и на комплексной плоскости. В этом случае все хорды являются векторами (рис.12.5).
На комплексной плоскости совместим хорду CA =  с вещественной осью.
с вещественной осью.
Если  > 0, то от продолжения хорды он должен быть отложен против часовой стрелки.
> 0, то от продолжения хорды он должен быть отложен против часовой стрелки.
 | Обозначим DA = 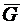 ; и ; и  . Тогда . Тогда
Вектор
Если k = 0, то При k = ∞
|
Подставляя (12.10) в (12.9), получаем
 или или  , , | (12.11) |
откуда
 | (12.12) |
Уравнение (12.12) называют уравнением дуги окружности в векторной форме.
При изменении коэффициента k от 0 до ∞ изменяются оба вектора  и
и  , но так, что угол
, но так, что угол  между ними остается неизменным, а сумма векторов равна вектору
между ними остается неизменным, а сумма векторов равна вектору  .
.
Конец вектора  скользит по дуге окружности, хордой которой является вектор
скользит по дуге окружности, хордой которой является вектор 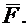 Поэтому можно считать, что дуга окружности является геометрическим местом концов вектора
Поэтому можно считать, что дуга окружности является геометрическим местом концов вектора 
Если процесс в электрической цепи описывается уравнением по форме тождественным уравнению (12.12), то геометрическим местом концов вектора тока или напряжения, выполняющего в уравнении цепи ту же роль, что и вектор  в уравнении (12.12), является дуга окружности.
в уравнении (12.12), является дуга окружности.
Под круговой диаграммой тока или напряжения понимают дугу окружности, являющуюся геометрическим местом концов вектора тока или напряжения при изменении по модулю какого-либо сопротивления цепи и сохранении неизменными остальных сопротивлений, ЭДС и частоты.
Круговая диаграмма тока для двух последовательно
 2018-02-13
2018-02-13 2274
2274

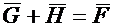
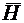 опережает вектор
опережает вектор 
 и
и  .
.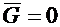 и
и 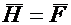 .
.