Дифференциальные уравнения длинной линии

Основные понятия и определения

Электрические цепи, в которых ток и напряжение непрерывно изменяются при переходе от одной точке цепи к другой, называются цепями с распределенными параметрами.

До сих пор мы рассматривали электрические цепи с сосредоточенными параметрами, т. е. полагалось, что емкости сосредоточены в конденсаторах, индуктивности – в катушках, активные сопротивления также локализованы в виде отдельных элементов – резисторов. При таком представлении электрической цепи считают, что ток, входящий в любой элемент, равен току, выходящему из того же элемента; что во всех точках любой ветви цепи ток имеет одну и ту же величину и фазу; что падение напряжения вдоль любого соединительного проводника равно нулю. Электрическое и магнитное поля считают сосредоточенными в конденсаторах и катушках соответственно, причем не учитываются ЭДС самоиндукции, возникающие во всей системе под влиянием переменного магнитного поля, пересекающего соединительные провода; токи смещения между отдельными проводниками и между витками катушек; токи проводимости (утечки) между проводниками цепи и обкладками конденсаторов, обусловленные несовершенством разделяющих их диэлектриков. Однако замена электротехнического устройства цепью с сосредоточенными параметрами неправомерна в ряде случаев: а) при расчете длинной линии электропередачи или связи; б) в случае работы устройства на разных частотах.

Все дальнейшие расчеты и выводы будем проводить на примере длинной линии электропередачи. Участок такой линии может быть представлен эквивалентной цепочечной схемой, представленной на рисунке 28.1.

 

 

На схеме (рис. 28.1,а) сопротивления Z ₁, Z ₂, Z ₃ называют продольными, с сопротивления Z ₄ – Z ₇ – поперечными.

Участок линии dx является бесконечно малым элементом длины линии.

В результате утечки тока через сопротивление Z ₄ ток i ₁ не равен току i, а напряжение на участке ab не равно напряжению на участке cd и т.д.

В двухпроводной линии (рис. 28.1,б) продольные сопротивления образованы активными сопротивлениями проводов и индуктивностью участка линии. Поперечные сопротивления состоят из сопротивлений (или проводимостей), учитывающих утечку тока через изоляцию и емкостью между проводами линии.

Для достаточно длинной линии можно считать, что эти параметры распределены вдоль линии равномерно. Такую линию считают однородной.

Параметры линии на единицу длины обозначают R ₀, L ₀, G ₀ и C ₀.

 

Дифференциальные уравнения длинной линии

 

В цепях с сосредоточенными параметрами напряжение и ток в элементах связаны соотношениями:

    ; 

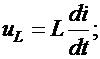
Решение этих уравнений дает закон изменения тока и напряжения от времени, но не от координаты длины линии. Если выделить какой-то участок цепи с распределенными параметрами, то токи и напряжения на концах этого участка не будут равны токам и напряжениям в его начале. Только при бесконечном уменьшении длины участка эти величины равны.

Следовательно, приведенные выше выражения непосредственно не применимы ко всей линии в целом. Они могут быть применены только к бесконечно малым по длине участкам.

Напряжения и токи в линии являются функциями двух независимых переменных: пространственной координаты х (вдоль линии) и времени t. Отсюда вытекает задача определения тока и напряжения как функций двух переменных: u = f (x, t); i = f (x, t).

На рисунке 28.2 изображена схема короткого отрезка Δ х двухпроводной линии.

Рассмотрим две точки с координатами х и х +Δ х. Обозначим соответствующие этим точкам напряжения и токи для любого фиксированного момента времени через u = u (x), u (x +Δ x), i = i (x) и i (x +Δ x). Напряжение u (x +Δ x) отличается от напряжения u (x), так как на участке Δ х происходит падение напряжения на индуктивности L ₀Δ х и сопротивлении R ₀Δ x. Поэтому можно записать

.

Это и последующие уравнения записаны в частных производных, так как ток и напряжение являются функциями двух переменных t и x.

Соответственно изменение тока на участке Δ х происходит за счет ответвления тока через емкость C₀ Δ x и проводимость изоляции G₀ Δ x между проводами:

Эти два равенства переписываются следующим образом:

,  

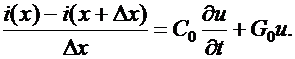
Переходя к пределу при 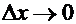, получаем в соответствии с определением производной:

	(28.1)
	(28.2)

 

Знаки в левых частях выражений (28.1) и (28.2) обусловлены выбором положительных направлений.

Уравнения (28.1), (28.2) являются основными дифференциальными уравнениями для линии с распределенными параметрами. Они могут быть решены однозначно при использовании начальных и граничных условий.

В качестве начальных условий могут использоваться значения тока и напряжения в начале (или конце) линии в момент t = 0.

Граничные условия определяются связями между напряжением и током в начале или конце линии, зависящими от заданного режима работы линии.