Принцип непрерывности магнитного потока

Под магнитным потоком понимают поток вектора магнитной индукции через некоторую поверхность:

(43.8)

Магнитный поток измеряется в веберах (вб).

Магнитную индукцию можно определить как плотность магнитного потока. Если площадь S перпендикулярна вектору 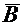и поле однородное, то

Установлено, что магнитный поток сквозь замкнутую поверхность всегда равен нулю:

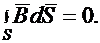
(43.9)

Пользуясь теоремой Остроградского, можно записать:

Так как это равенство справедливо для любого объема, то

(43.10)

Последняя формула выражает принцип непрерывности магнитного потока в дифференциальной форме. Она означает, что линии магнитной индукции не имеют ни истоков, ни стоков и являются замкнутыми сами на себя линиями.

Скалярный потенциал магнитного поля

Для совокупности точек, где , , 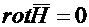магнитное поле можно рассматривать как потенциальное, т.е. как поле, каждая точка которого имеет скалярный магнитный потенциал φ_м. Следовательно, для таких областей можно принять

(43.11)

Так как то при имеем . Подставив в последнее выражение вместо , получим . Таким образом, скалярный потенциал магнитного поля подчиняется уравнению Лапласа.

Граничные условия в магнитном поле постоянного тока

Подобно тому, как в электростатическом поле и в поле проводящей среды выполнялись определенные граничные условия, в магнитном поле также имеют место аналогичные условия:

	(43.12)
	(43.13)

Условие (43.12) означает, что на границе раздела двух однородных и изотропных сред, отличающихся значением магнитной проницаемости _,равны тангенциальные составляющие напряженности магнитного поля.