Плоская электромагнитная волна

Уравнения Максвелла для проводящей среды

Уравнения Максвелла в комплексной форме для синусоидально изменяющихся во времени Е и Н

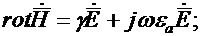В проводящей среде даже при очень высоких частотах произведение  много меньше проводимости  Поэтому слагаемым  в первом уравнении Максвелла для проводящих сред можно пренебречь.

При таком допущении уравнения Максвелла для проводящей среды принимают вид:

	(46.1)
	(46.2)

В этих уравнениях два неизвестных  и 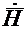. Для их нахождения возьмем ротор от уравнения (46.1):

Учтем, что  Вместо 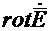 в соответствии с (46.2) подставим  Получим

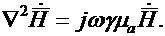(46.3)

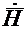Последнее уравнение является дифференциальным относительно  В общем случае, когда  зависит от всех трех или даже только от двух координат, его решение довольно сложно. Поэтому рассмотрим его решение для частного случая – для плоской электромагнитной волны.

 

Плоская электромагнитная волна

 

Под плоской электромагнитной волной понимают волну, векторы 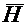 и 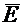 которой расположены в плоскости xOy, перпендикулярной направлению распространения волны (ось z), и изменяются только в функции координаты z и времени t. В дальнейшем под плоской волной будем понимать плоскую линейно поляризованную вол ну, в которой вектор  направлен вдоль одной, а вектор 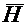 – вдоль другой координатной оси плоскости xOy.

В силу определения плоской волны:

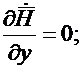
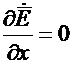   и

В плоской волне  и 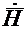 являются функциями только одной координаты – функцией только z.

Повернем координатные оси таким образом, чтобы ось y совпала с вектором напряженности магнитного поля 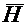. При этом , где 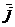 – единичный орт оси y декартовой системы координат. Подставим  в уравнение (27.3) и раскроем :

(46.4)

Учитывая, что

 и

получаем

(46.5)

Уравнение (46.5) является линейным дифференциальным уравнением второго порядка. Его решение имеет следующий вид:

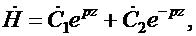(46.6)

где  и  – постоянные интегрирования; это комплексы, которые определяются из граничных условий; для каждой конкретной задачи свои постоянные. Из характеристического уравнения 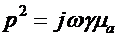 найдем постоянную распространения

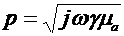(46.7)

 

 

Так как

то р можно представить и так:

(46.8)

где

(46.9)

Найдем  В соответствии с уравнением (46.6) имеем

(46.10)

Следовательно,

(46.10,а)

Производная

.

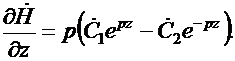(46.11)

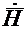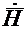Выражение (46.10,а) показывает, что вектор напряженности электрического поля в плоской волне при выбранном расположении координатных осей направлен вдоль оси x (орт ). Таким образом, в плоской электромагнитной волне между  и  имеется пространственный сдвиг в  (  направлено по оси x, а  – по оси y).

Частное от деления p на γ принято называть волновым сопротивлением:

(46.12)

Волновое сопротивление измеряется в омах, зависит от свойств среды (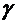  и ) и угловой частоты . В соответствие с (46.10,а) и (46.11) проекция  на ось x равна

где

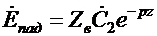 и

Проекция  на ось y в соответствии с (46.6)

где

 и

Компоненты падающе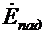й  и  волны определяют вектор Пойнтинга , направленный вдоль положительного направления оси z. Следовательно, движение энергии падающей волны происходит вдоль положительного направления оси z. Компоненты отраженной волны  и  определяют вектор Пойтинга , направленный вдоль отрицательного направления оси z. Это означает, что отраженная волна несет с собой энергию вдоль отрицательного направления оси z. Волновое сопротивление  можно трактовать как отношение . Волновое сопротивление является числом комплексным и имеет аргумент , поэтому сдвиг во времени между 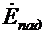 и  для одной и той же точки поля тоже равен .